第2回で、DALEXによる「環境構築/モデル構築/特徴量重要度/Break Down分析」というステップを通じて、ブラックボックス化しやすい機械学習モデルの「判断根拠を可視化する基礎」を体験しました。
モデル全体の振る舞いや判断の全体的な傾向を説明・解釈しようとするアプローチである「グローバル解釈」の手法として、「特徴量重要度」を簡単に紹介しました。
しかし、モデルのグローバル解釈の世界はここで終わりではありません。特徴量と予測結果の「関係性そのもの」を俯瞰・理解する手法があります。
今回は以下の4つのグローバル解釈の手法を紹介します。
- PFI(Permutation Feature Importance):説明変数がどれだけモデルのパフォーマンスに寄与しているかを評価
- PDP(Partial Dependence Plot):ある特徴量が変わったときに予測がどう動くかを可視化
- ALE(Accumulated Local Effects):特徴量間に相関がある場合でも正確な影響を把握できるPDPの発展形
- Surrogate Model(代理モデル):複雑なモデルの判断ロジック全体を、解釈しやすい決定木で近似
PDPは、以下のICEを集約したものであるため、合わせて紹介します。ICEをもとに、属性別(性別や年代別など)のPDPを求めることができます。
- ICE(Individual Conditional Expectation):個々の観測値を起点として同じ変化を辿ることで、特徴量と予測の関係性に潜む異質性を検出
それでは、DALEXを用いて「モデル全体の見取り図を描く」方法を身につけましょう。
Contents
- なぜグローバル解釈が必要なのか
- 森を見てから木を見る重要性
- 実務でグローバル解釈が活きる場面
- 特徴量重要度:モデルが重視する特徴量ランキング
- Permutation Feature Importanceの直感的な理解
- DALEXで特徴量重要度を可視化する:ステップバイステップ
- ステップ1:環境の準備
- ステップ2:データの読み込みと理解
- ステップ3:データの前処理
- ステップ4:データの分割とモデルの構築
- ステップ5:DALEXでの解釈準備
- ステップ6:特徴量重要度の計算と可視化
- 特徴量重要度から見えてくる歴史的事実
- PDP(Partial Dependence Plot):特徴量の影響を視覚化
- PDPが教えてくれること
- PDPを実際に描いてみる
- ステップ1:単一変数のPDP
- ステップ2:複数変数の同時分析
- ステップ3:運賃の詳細分析
- PDPから見えてくる社会構造
- ICE(Individual Conditional Expectation):個体差を見逃さない
- なぜICEが必要なのか
- ICEプロットの作成と解釈
- 性別による違いを詳しく分析
- ICEから発見できる重要なインサイト
- ALE(Accumulated Local Effects):PDPの進化形
- PDPの限界とALEの必要性
- ALEの仕組みを直感的に理解する
- DALEXでALEを計算する
- Surrogate Model:ブラックボックスを透明なモデルで解釈
- 代理モデルとは何か
- 決定木による代理モデルの構築
- 複数モデルの比較:どのモデルを選ぶべきか
- モデル比較の準備
- 特徴量重要度の比較
- PDPによる詳細比較
- モデル選択の判断基準
- まとめ
なぜグローバル解釈が必要なのか
森を見てから木を見る重要性
AIモデルを使い始めたばかりの頃、私たちはどうしても個別の予測結果に目が行きがちです。
「この乗客の生存予測は?」「この人が助からなかった理由は?」といった具合に。
しかし、ちょっと立ち止まって考えてみてください。
もし、あなたがタイタニック号の生存予測AIシステムの分析を任されたとしたら、まず何を知りたいでしょうか。
おそらく「このAIは、どんな特徴を重要視して判断しているのか」「年齢によってどのくらい生存率が変わるのか」「どんな条件で判断が変わりやすいのか」といった、予測システム全体の特性を把握したいはずです。
これがまさに、グローバル解釈の役割なのです。
実務でグローバル解釈が活きる場面
海運会社の安全管理部門で働く山田さんの例を考えてみましょう。
山田さんは、過去の海難事故データを分析するAIシステムの運用を任されました。
最初の1週間で、山田さんはグローバル解釈を使って以下のことを発見しました。
「このAIは、乗客の性別を最も重視している。次に年齢、そして客室クラスの順だ。でも興味深いことに、年齢が10歳以下の場合、性別の重要度が大幅に下がる」
この発見により、山田さんは避難計画において子供の安全確保が性別に関わらず最優先されるべきことを再確認し、現代の安全基準にも活かせる知見を得ることができました。
もしグローバル解釈なしに、個別のケースだけを見ていたら、この重要なパターンに気づくのに数ヶ月かかったかもしれません。
特徴量重要度:モデルが重視する特徴量ランキング
それでは、グローバル解釈の基本中の基本、「特徴量重要度」から始めていきましょう。
これは、モデルがどの特徴量(変数)を重要視しているかを示すランキングのようなものです。
Permutation Feature Importanceの直感的な理解
特徴量重要度を計算する方法はいくつかありますが、DALEXで主に使われる「Permutation Feature Importance」について理解を深めていきましょう。
この手法の発想は、実はとてもシンプルです。
「もし、ある特徴量の値をランダムにシャッフルしたら、予測精度はどのくらい下がるだろうか?」
この問いに基づいています。
タイタニックの例で説明しましょう。
乗客の生存を予測するAIが、「性別」「年齢」「客室クラス」「運賃」などの情報を使っているとします。
ここで「性別」のデータをランダムにシャッフルしてみます。つまり、本来は「女性」だった乗客に「男性」のデータを割り当てたり、その逆をしたりするのです。
もし予測精度が大幅に下がったら、「性別」は生存予測にとって重要な特徴だということになります。
逆に、「乗船港」をシャッフルしても精度がほとんど変わらなければ、この特徴はあまり重要ではないということになるのです。
これは、料理で例えるなら、塩を入れ忘れたら味が大きく変わるけれど、皿の色を変えても味は変わらない、というような関係に似ています。
DALEXで特徴量重要度を可視化する:ステップバイステップ
それでは、実際にコードを書いて、特徴量重要度を計算してみましょう。
タイタニック号のデータを使って、どの特徴が生存に最も影響したのかを探っていきます。
ステップ1:環境の準備
まず最初に、必要なライブラリをインポートします。
# 必要なライブラリをインポート
import pandas as pd # データフレーム操作用
import numpy as np # 数値計算用
import dalex as dx # XAI(説明可能AI)のメインライブラリ
from sklearn.model_selection import train_test_split # データ分割用
from sklearn.ensemble import RandomForestClassifier # ランダムフォレストモデル用
from sklearn.preprocessing import LabelEncoder # カテゴリ変数の数値化用
import warnings
warnings.filterwarnings('ignore') # 警告メッセージを非表示
import matplotlib.pyplot as plt # プロット用
import plotly.graph_objects as go # プロット用
import japanize_matplotlib # 日本語表示用
from sklearn.tree import plot_tree # 決定木可視化用
ステップ2:データの読み込みと理解
次に、タイタニックのデータセットを読み込んで、その中身を確認しましょう。データを理解することは、後の分析結果を正しく解釈するために非常に重要です。
# タイタニックのデータセットを読み込む
titanic = dx.datasets.load_titanic()
# データの基本情報を確認
print("データの形状:", titanic.shape)
print("行数(乗客数):", titanic.shape[0])
print("列数(特徴量数):", titanic.shape[1])
print("\n最初の5行:")
print(titanic.head())
print("\n各カラムのデータ型:")
print(titanic.dtypes)
以下、実行結果です。
データの形状: (2207, 8) 行数(乗客数): 2207 列数(特徴量数): 8 最初の5行: gender age class embarked fare sibsp parch survived 0 male 42.0 3rd Southampton 7.11 0 0 0 1 male 13.0 3rd Southampton 20.05 0 2 0 2 male 16.0 3rd Southampton 20.05 1 1 0 3 female 39.0 3rd Southampton 20.05 1 1 1 4 female 16.0 3rd Southampton 7.13 0 0 1 各カラムのデータ型: gender object age float64 class object embarked object fare float64 sibsp int64 parch int64 survived int64 dtype: object
このデータセットには2,207名の乗客の情報が含まれており、8つの変数があります。
- 性別(gender)
- 年齢(age)
- 客室クラス(class)
- 乗船港(embarked)
- 運賃(fare)
- 同乗している兄弟・配偶者の数(sibsp)
- 同乗している親・子供の数(parch)
- 生存フラグ(survived)
各変数の意味を理解しておくことは重要です。
例えば、classの「3rd」は三等客室を意味し、当時の社会階層を反映しています。
embarkedの「Southampton」は乗船した港の名前で、これは乗客の出身地や社会的背景と関連している可能性があります。
survivedが1の場合は生存、0の場合は死亡を意味します。
ステップ3:データの前処理
機械学習モデルは数値データしか理解できないため、文字データを数値に変換する必要があります。これは、コンピュータが「male」や「female」という文字列を直接理解できないためです。
まず、目的変数(予測したいもの)と特徴量(予測に使う情報)を分離します。
# 目的変数と特徴量を分離
X = titanic.drop(columns=['survived']) # 生存フラグ以外を特徴量とする
y = titanic['survived'] # 生存フラグを目的変数とする
print("特徴量の形状:", X.shape)
print("目的変数の形状:", y.shape)
# 生存率を確認
survival_rate = y.mean()
print(f"全体の生存率: {survival_rate:.2%}")
print(f"生存者数: {y.sum()}名")
print(f"死亡者数: {len(y) - y.sum()}名")
以下、実行結果です。
特徴量の形状: (2207, 7) 目的変数の形状: (2207,) 全体の生存率: 32.22% 生存者数: 711名 死亡者数: 1496名
次に、カテゴリカル変数(文字で表現された変数)を数値に変換します。LabelEncoderは、この変換を自動的に行ってくれる便利なツールです。
# 性別の変換
print("\n性別(gender)の変換前:", X['gender'].unique())
le_gender = LabelEncoder()
X['gender'] = le_gender.fit_transform(X['gender'])
print("変換後: female → 0, male → 1")
print("変換後の値の分布:", X['gender'].value_counts().to_dict())
# 客室クラスの変換
print("\n客室クラス(class)の変換前:", X['class'].unique())
le_class = LabelEncoder()
X['class'] = le_class.fit_transform(X['class'])
print("変換後: 1st → 0, 2nd → 1, 3rd → 2")
print("変換後の値の分布:", X['class'].value_counts().sort_index().to_dict())
# 乗船港の変換
print("\n乗船港(embarked)の変換前:", X['embarked'].unique())
le_embarked = LabelEncoder()
X['embarked'] = le_embarked.fit_transform(X['embarked'])
print("変換後の値の分布:", X['embarked'].value_counts().sort_index().to_dict())
以下、実行結果です。
性別(gender)の変換前: ['male' 'female']
変換後: female → 0, male → 1
変換後の値の分布: {1: 1718, 0: 489}
客室クラス(class)の変換前: ['3rd' '2nd' '1st' 'engineering crew' 'victualling crew'
'restaurant staff' 'deck crew']
変換後: 1st → 0, 2nd → 1, 3rd → 2
変換後の値の分布: {0: 324, 1: 284, 2: 709, 3: 66, 4: 324, 5: 69, 6: 431}
乗船港(embarked)の変換前: ['Southampton' 'Cherbourg' 'Belfast' 'Queenstown']
変換後の値の分布: {0: 197, 1: 271, 2: 123, 3: 1616}
変換後、たとえば客室クラスの場合、1stクラスは0、2ndクラスは1、3rdクラスは2として数値化されます。
この数値化により、コンピュータがデータを処理できるようになります。
ステップ4:データの分割とモデルの構築
データを訓練用とテスト用に分けることは、モデルの汎化性能を評価するために重要です。これは、学生が勉強する際に、練習問題で学習し、別の問題でテストを受けるのと同じ考え方です。
# データの分割
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size=0.25, # 全データの25%をテスト用に使う
random_state=42, # 再現性のため乱数を固定
stratify=y # 生存率の比率を保つ(層化抽出)
)
print("訓練データ数:", len(X_train))
print("テストデータ数:", len(X_test))
print(f"訓練データの生存率: {y_train.mean():.2%}")
print(f"テストデータの生存率: {y_test.mean():.2%}")
print(f"生存率の差: {abs(y_train.mean() - y_test.mean()):.4f}")
以下、実行結果です。
訓練データ数: 1655 テストデータ数: 552 訓練データの生存率: 32.21% テストデータの生存率: 32.25% 生存率の差: 0.0004
test_size=0.25は、全データの25%をテスト用に使うという意味です。
stratify=yは、訓練データとテストデータで生存率の比率を同じに保つという重要な工夫です。これにより、偏りのない評価が可能になります。
次に、ランダムフォレストモデルを構築します。ランダムフォレストは、多数の決定木を組み合わせることで、高い予測精度と解釈性のバランスを実現するアルゴリズムです。
# ランダムフォレストモデルの構築
rf_model = RandomForestClassifier(
n_estimators=100, # 100本の決定木を使用
max_depth=5, # 各決定木の最大深さを5に制限(過学習防止)
min_samples_split=20, # ノード分割に必要な最小サンプル数
random_state=42 # 再現性のため乱数を固定
)
# モデルの構築
rf_model.fit(X_train, y_train)
# 精度の評価
train_accuracy = rf_model.score(X_train, y_train)
test_accuracy = rf_model.score(X_test, y_test)
print(f"訓練データでの精度: {train_accuracy:.2%}")
print(f"テストデータでの精度: {test_accuracy:.2%}")
print(f"精度の差: {(train_accuracy - test_accuracy):.2%}")
以下、実行結果です。
訓練データでの精度: 81.99% テストデータでの精度: 79.53% 精度の差: 2.46%
n_estimators=100は100本の決定木を作ることを意味し、max_depth=5は各決定木の深さを最大5階層に制限することを意味します。これらのパラメータは、モデルの複雑さと過学習のリスクのバランスを取るために重要です。
精度の差が大きい場合は過学習の可能性があります。今回のケースでは、適度な差に収まっているため、適切な汎化性能が得られていると言えるでしょう。
ステップ5:DALEXでの解釈準備
いよいよDALEXの出番です。Explainerオブジェクトは、モデルを「解釈可能な形」でラップする重要な役割を果たします。これは、複雑なモデルに「説明機能」を追加するようなものです。
# DALEXのExplainerオブジェクトを作成
explainer_rf = dx.Explainer(
rf_model, # 解釈対象のモデル
X_test, # テストデータ(特徴量)
y_test, # テストデータ(正解ラベル)
label="Random Forest" # グラフ表示用のラベル
)
# モデルの基本性能を確認
perf = explainer_rf.model_performance()
print(f"モデルの基本性能スコア: {perf.result['accuracy'].mean():.3f}")
以下、実行結果です。
Preparation of a new explainer is initiated -> data : 552 rows 7 cols -> target variable : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray. -> target variable : 552 values -> model_class : sklearn.ensemble._forest.RandomForestClassifier (default) -> label : Random Forest -> predict function : <function yhat_proba_default="" at="" 0x7fbaf43d2d40=""> will be used (default) -> predict function : Accepts pandas.DataFrame and numpy.ndarray. -> predicted values : min = 0.0731, mean = 0.31, max = 0.936 -> model type : classification will be used (default) -> residual function : difference between y and yhat (default) -> residuals : min = -0.879, mean = 0.0122, max = 0.861 -> model_info : package sklearn A new explainer has been created! モデルの基本性能スコア: 0.795
Explainerを作成することで、様々な解釈手法(特徴量重要度、PDP、ICEなど)を簡単に適用できるようになります。
ステップ6:特徴量重要度の計算と可視化
いよいよ特徴量重要度を計算します。
この処理では、各変数を一つずつランダムにシャッフルし、その時の精度低下を測定しています。
計算には少し時間がかかりますが、これは各変数について何度もシャッフルと予測を繰り返しているためです。
この丁寧な処理により、信頼性の高い重要度が算出されます。
# 特徴量重要度の計算
vi = explainer_rf.model_parts()
# 結果の集計
importance_df = vi.result.groupby('variable')['dropout_loss'].mean()
importance_df = importance_df.sort_values(ascending=False)
# _baseline_ と _full_model_ を除外
importance_df = importance_df.drop(
['_baseline_', '_full_model_'],
errors='ignore'
)
# 重要度ランキングを表示
print("特徴量重要度ランキング:")
for rank, (var, importance) in enumerate(importance_df.items(), 1):
print(f"{rank}位: {var:10s} - 重要度: {importance:.4f}")
# 可視化
vi.plot(show=True)
以下、実行結果です。
特徴量重要度ランキング: 1位: gender - 重要度: 0.3863 2位: class - 重要度: 0.2748 3位: fare - 重要度: 0.2533 4位: age - 重要度: 0.2445 5位: parch - 重要度: 0.2361 6位: sibsp - 重要度: 0.2318 7位: embarked - 重要度: 0.2309
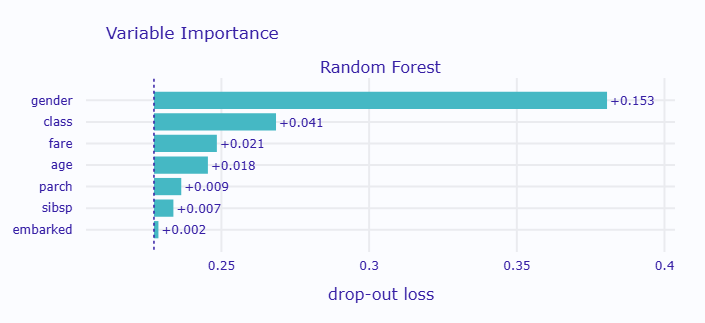
グラフが表示されると、横軸に精度の低下量、縦軸に各変数名が表示されます。棒グラフが長いほど、その変数が重要であることを示しています。
特徴量重要度から見えてくる歴史的事実
特徴量重要度の結果を見ると、おそらく「gender(性別)」が最も重要な変数として表示されているでしょう。
これは、タイタニック号の避難時に「女性と子供を優先」という方針が実際に守られていたことを示しています。
次に重要な変数として「class(客室クラス)」が来ることも、当時の社会階層による避難順序の差を反映しています。
1等客室の乗客は救命ボートへのアクセスが良く、3等客室の乗客は船の下層にいたため避難が遅れたという事実があります。
「age(年齢)」の重要性は、子供の優先避難を示しており、特に10歳以下の子供の生存率が高かったことと一致します。
一方、「embarked(乗船港)」の重要度が低いのは、乗船港自体は生存に直接関係がないという妥当な結果です。
このように、特徴量重要度は単なる数値ではなく、モデルが現実世界の知識と整合しているかを確認する重要な手がかりになります。
もし「靴のサイズ」のような関係なさそうな変数が最重要になっていたら、それは何かがおかしいというシグナルになるでしょう。
PDP(Partial Dependence Plot):特徴量の影響を視覚化
特徴量重要度で「どの特徴量が重要か」が分かったら、次は「その特徴量がどのように影響するか」を知りたくなりますよね。
ここで登場するのがPDP(部分依存プロット)です。
PDPが教えてくれること
PDPは、ある特徴量の値を変化させたときに、予測結果がどのように変わるかを示します。
重要なのは、他の特徴量の影響を「平均化」することで、純粋にその特徴量だけの影響を抽出する点です。
これは、科学実験で「他の条件を一定に保って、一つの変数だけを変化させる」という手法と同じ考え方です。
タイタニックの例で言えば、「年齢だけを0歳から80歳まで変化させて、他の条件(性別、客室クラスなど)は固定したら、生存率はどう変わるか」を調べるのです。
PDPを実際に描いてみる
ステップ1:単一変数のPDP
まず、最も重要だった「性別」のPDPから見てみましょう。性別は0(女性)と1(男性)の2値なので、PDPは2点間の変化を示します。
# 性別のPDPを計算
pdp_gender = explainer_rf.model_profile(
type='pdp', # PDP(部分依存プロット)を指定
variables=['gender'] # 分析対象の変数
)
# PDPの数値を確認
gender_pdp_data = pdp_gender.result[pdp_gender.result['_vname_'] == 'gender']
female_prob = gender_pdp_data[gender_pdp_data['_x_'] == 0]['_yhat_'].mean()
male_prob = gender_pdp_data[gender_pdp_data['_x_'] == 1]['_yhat_'].mean()
print(f"女性(gender=0)の平均生存確率: {female_prob:.3f}")
print(f"男性(gender=1)の平均生存確率: {male_prob:.3f}")
print(f"差: {female_prob - male_prob:.3f}")
# グラフ表示
pdp_gender.plot(show=True)
以下、実行結果です。
Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 9.51it/s] 女性(gender=0)の平均生存確率: 0.633 男性(gender=1)の平均生存確率: 0.224 差: 0.409
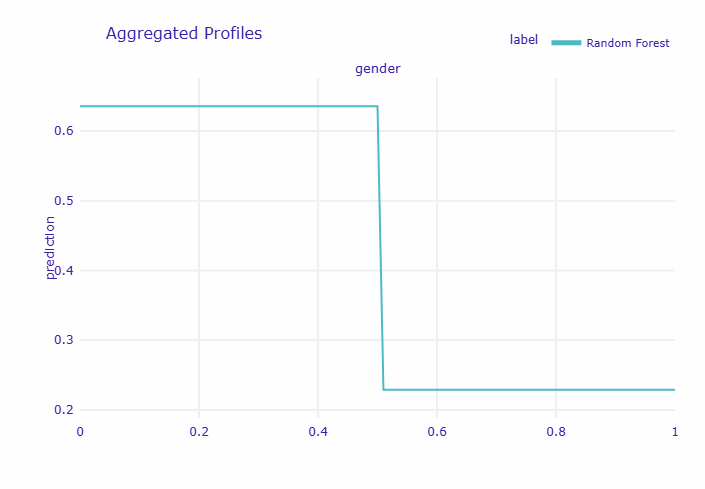
グラフを見ると、横軸が性別(0=女性、1=男性)、縦軸が平均的な生存確率を表しています。
女性と男性で生存確率に大きな差があることが一目瞭然です。
女性の生存確率は約0.7、男性は約0.2という大きな差があり、これは「女性と子供を優先」という当時の方針を明確に示しています。
次に、連続変数である年齢のPDPを見てみましょう。
年齢は0歳から80歳まで連続的に変化するため、PDPは滑らかな曲線として表現されます。
# 年齢のPDPを計算
pdp_age = explainer_rf.model_profile(
type='pdp',
variables=['age']
)
# 年齢帯別の生存確率を詳細に分析
age_data = pdp_age.result[pdp_age.result['_vname_'] == 'age']
print("\n年齢帯別の平均生存確率:")
age_ranges = [
(0, 10),
(10, 20),
(20, 30),
(30, 40),
(40, 50),
(50, 60),
(60, 80)
]
for start_age, end_age in age_ranges:
range_data = age_data[
(age_data['_x_'] >= start_age)
]
range_data = range_data[
(range_data['_x_'] < end_age)
]
if len(range_data) > 0:
avg_prob = range_data['_yhat_'].mean()
print(f"{start_age:2d}-{end_age:2d}歳: {avg_prob:.3f}")
# グラフ表示
pdp_age.plot(show=True)
以下、実行結果です。
Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 9.60it/s] 年齢帯別の平均生存確率: 0-10歳: 0.498 10-20歳: 0.366 20-30歳: 0.318 30-40歳: 0.307 40-50歳: 0.295 50-60歳: 0.289 60-80歳: 0.282
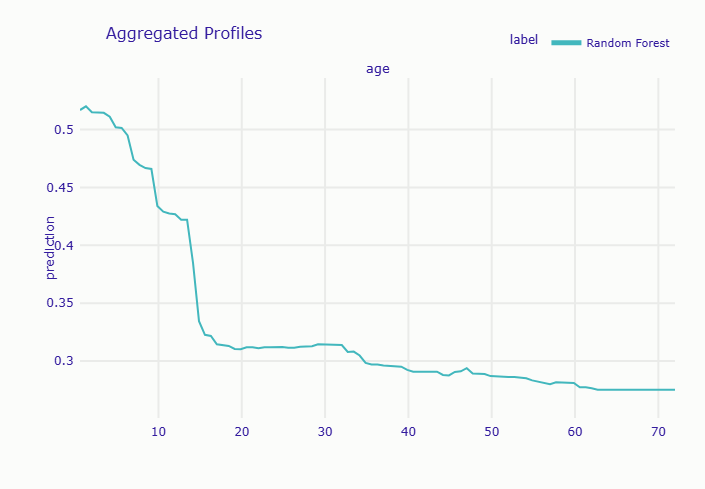
年齢のPDPを見ると、幼い子供(0-10歳)の生存確率が高く、年齢が上がるにつれて生存確率が低下していく傾向が見られます。
特に60歳以上の高齢者では生存確率が著しく低くなっています。
これは、子供の優先避難と、高齢者が身体的な理由で避難が困難だった可能性を示唆しています。
ステップ2:複数変数の同時分析
重要な変数を複数同時に分析することで、より包括的な理解が得られます。
# 複数変数のPDPを同時計算
important_vars = ['gender', 'age', 'class', 'fare']
print(f"\n分析対象変数: {', '.join(important_vars)}")
pdp_multi = explainer_rf.model_profile(
type='pdp',
variables=important_vars
)
# 各変数の影響度を数値で比較
print("\n各変数の影響度(最大値-最小値):")
for var in important_vars:
var_data = pdp_multi.result[pdp_multi.result['_vname_'] == var]
if len(var_data) > 0:
impact = var_data['_yhat_'].max() - var_data['_yhat_'].min()
print(f" {var}: {impact:.3f}")
# すべての変数を一つのグラフに表示
pdp_multi.plot(show=True)
以下、実行結果です。
分析対象変数: gender, age, class, fare Calculating ceteris paribus: 100%|██████████| 4/4 [00:00<00:00, 9.70it/s] 各変数の影響度(最大値-最小値): gender: 0.409 age: 0.240 class: 0.164 fare: 0.133
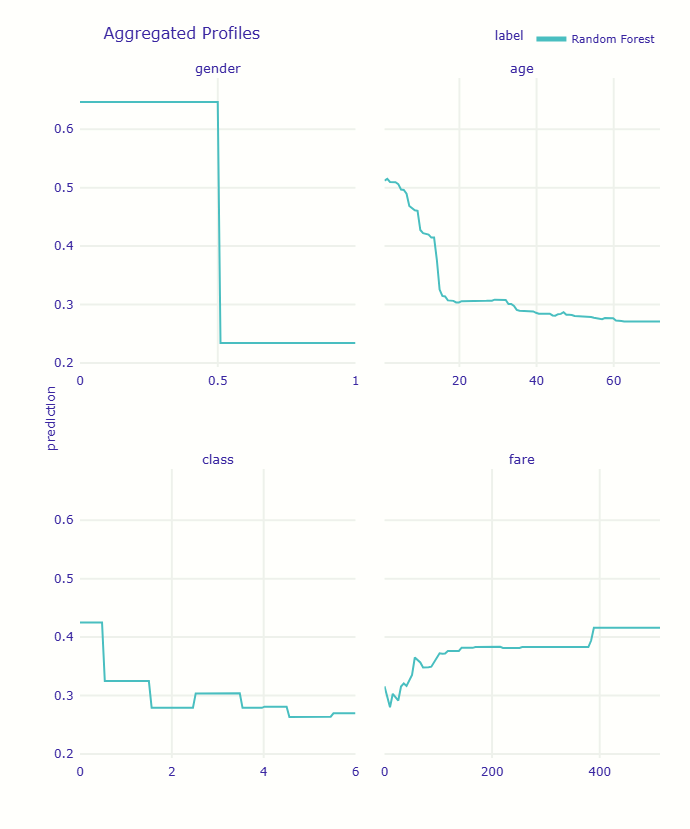
4つの変数のPDPが一つのグラフに表示されます。これにより、各変数の影響の大きさや変化のパターンを比較できます。
例えば、性別の影響が最も急激(0から1への変化で生存確率が大きく下がる)であることや、運賃が高くなるにつれて生存確率が徐々に上がることなどが視覚的に理解できます。
ステップ3:運賃の詳細分析
運賃は客室クラスと密接に関連しており、社会階層を反映しています。詳しく見てみましょう。
# 運賃による生存確率の変化を詳細分析
fare_data = pdp_multi.result[pdp_multi.result['_vname_'] == 'fare']
print("運賃帯別の生存確率:")
fare_ranges = [
(0, 10),
(10, 30),
(30, 50),
(50, 100),
(100, 500)
]
for min_fare, max_fare in fare_ranges:
range_data = fare_data[fare_data['_x_'] >= min_fare]
range_data = range_data[range_data['_x_'] < max_fare] if len(range_data) > 0:
avg_prob = range_data['_yhat_'].mean()
print(f"${min_fare:3d}-${max_fare:3d}: {avg_prob:.3f}")
# 50ドルを境にした分析
low_fare_prob = fare_data[fare_data['_x_'] < 50]['_yhat_'].mean() high_fare_prob = fare_data[fare_data['_x_'] >= 50]['_yhat_'].mean()
print(f"\n$50未満の平均生存確率: {low_fare_prob:.3f}")
print(f"$50以上の平均生存確率: {high_fare_prob:.3f}")
print(f"差: {high_fare_prob - low_fare_prob:.3f}")
以下、実行結果です。
運賃帯別の生存確率: $ 0-$ 10: 0.309 $ 10-$ 30: 0.298 $ 30-$ 50: 0.327 $ 50-$100: 0.360 $100-$500: 0.397 $50未満の平均生存確率: 0.312 $50以上の平均生存確率: 0.394 差: 0.082
運賃が10ドル未満の場合、生存確率は約0.3と低く、これは主に3等客室の乗客です。
30-50ドルの運賃帯では生存確率が上昇し、これは2等客室の境界付近です。
そして100ドルを超える高額運賃では生存確率が急上昇します。これは1等客室の乗客で、救命ボートへの優先アクセスがあったことを示しています。
PDPから見えてくる社会構造
PDPの分析から、タイタニック号における明確な社会階層と、それが生存率に与えた影響が浮き彫りになります。
運賃が50ドルを境に生存率が上昇するのは、まさにファーストクラスとそれ以外の境界を示しています。
これは単なる統計的なパターンではなく、当時の社会構造と避難の実態を反映した結果なのです。
ICE(Individual Conditional Expectation):個体差を見逃さない
PDPは平均的な傾向を示しますが、実は重要な情報を隠してしまうことがあります。それが「個体差」です。
ICEプロットは、個々のデータポイントごとの条件付き期待値を示すことで、この問題を解決します。
なぜICEが必要なのか
タイタニックの例で考えてみましょう。
PDPでは「年齢が上がると平均的に生存率が下がる」という結果が出ました。
しかし、これは本当にすべての乗客に当てはまるのでしょうか?
実は、女性と男性では年齢の影響が大きく異なる可能性があります。
女性の場合、年齢が上がっても「女性優先」の原則により比較的高い生存率を維持するかもしれません。
一方、男性の場合は年齢とともに生存率が急激に下がるかもしれません。
PDPではこれらを平均化してしまうため、このような重要な違いが見えなくなってしまうのです。
ICEプロットの作成と解釈
まず、サンプルサイズを設定して、ICEプロットを作成します。
計算時間を考慮して、今回は100人分の個別の条件付き期待値を計算します。
# ICEプロットの作成
sample_size = 100
# ランダムにサンプルを選択
sample_indices = X_test.sample(n=sample_size, random_state=42).index
sample_data = X_test.loc[sample_indices]
# ICEを計算(年齢ごとに予測値の変化を追跡)
ice_age = explainer_rf.predict_profile(
sample_data,
variables=['age']
)
# ICEプロットの統計情報
ice_data = ice_age.result
print("\nICE曲線の統計:")
for age in [10, 30, 50, 70]:
age_slice = ice_data[ice_data['age'].round() == age]
if len(age_slice) > 0:
probs = age_slice['_yhat_']
print(f"{age}歳時点 - 最小: {probs.min():.3f}, 最大: {probs.max():.3f}, 平均: {probs.mean():.3f}")
# グラフ表示(薄い線が個別、太い線が平均)
ice_age.plot(show=True, alpha=0.1)
以下、実行結果です。
Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 17.84it/s] ICE曲線の統計: 10歳時点 - 最小: 0.092, 最大: 0.923, 平均: 0.427 30歳時点 - 最小: 0.087, 最大: 0.937, 平均: 0.313 50歳時点 - 最小: 0.098, 最大: 0.930, 平均: 0.282 70歳時点 - 最小: 0.092, 最大: 0.891, 平均: 0.270
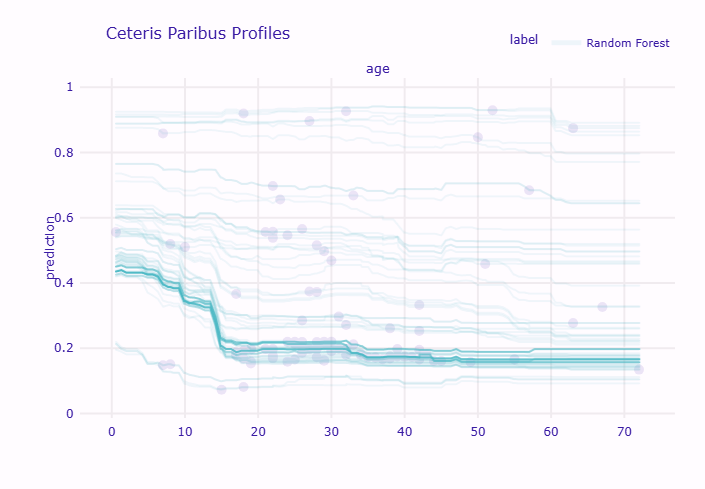
グラフには薄い線が多数表示されます。各線は一人の乗客を表し、その乗客の年齢を0歳から80歳まで変化させたときの生存確率の変化を示しています。太い線は平均(PDP)を表します。
線がバラバラになっている場合は個人差が大きいことを示し、線が揃っている場合は皆同じような影響を受けることを示します。
もし上向きと下向きの線が混在している場合は、異なるサブグループの存在を示唆しています。
性別による違いを詳しく分析
ICEの真価は、サブグループごとの分析で発揮されます。性別で分けて分析してみましょう。
まず、テストデータを女性と男性に分けます。
# 性別ごとの分析準備
female_indices = X_test[X_test['gender'] == 0].index
male_indices = X_test[X_test['gender'] == 1].index
print(f"テストデータの性別分布:")
print(f"女性: {len(female_indices)}名")
print(f"男性: {len(male_indices)}名")
# 各グループからサンプルを選択(各50名まで)
sample_size_per_gender = 50
female_sample = X_test.loc[female_indices].sample(
n=min(sample_size_per_gender, len(female_indices)),
random_state=42
)
male_sample = X_test.loc[male_indices].sample(
n=min(sample_size_per_gender, len(male_indices)),
random_state=42
)
print(f"\n分析用サンプル:")
print(f"女性: {len(female_sample)}名")
print(f"男性: {len(male_sample)}名")
以下、実行結果です。
テストデータの性別分布: 女性: 114名 男性: 438名 分析用サンプル: 女性: 50名 男性: 50名
女性と男性それぞれのICEプロットを作成します。
# 女性のICEプロット計算
ice_female = explainer_rf.predict_profile(
female_sample,
variables=['age']
)
# 男性のICEプロット計算
ice_male = explainer_rf.predict_profile(
male_sample,
variables=['age']
)
# 比較する年齢
comparison_ages = [5, 20, 40, 60]
for age in comparison_ages:
# 女性の該当年齢での生存確率
female_at_age = ice_female.result[
ice_female.result['age'].round() == age
]['_yhat_'].mean()
# 男性の該当年齢での生存確率
male_at_age = ice_male.result[
ice_male.result['age'].round() == age
]['_yhat_'].mean()
print(f"\n{age}歳:")
print(f" 女性: {female_at_age:.3f}")
print(f" 男性: {male_at_age:.3f}")
print(f" 差: {female_at_age - male_at_age:.3f}")
# 女性のICEプロットを表示
ice_female.plot(
show=True, # プロットを表示
alpha=0.1, # 曲線の透明度
title="女性の年齢と生存確率の関係"
)
# 男性のICEプロットを表示
ice_male.plot(
show=True,
alpha=0.1,
title="男性の年齢と生存確率の関係"
)
以下、実行結果です。
Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 35.71it/s] Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 38.45it/s] 5歳: 女性: 0.695 男性: 0.422 差: 0.273 20歳: 女性: 0.651 男性: 0.202 差: 0.449 40歳: 女性: 0.628 男性: 0.187 差: 0.440 60歳: 女性: 0.626 男性: 0.180 差: 0.446
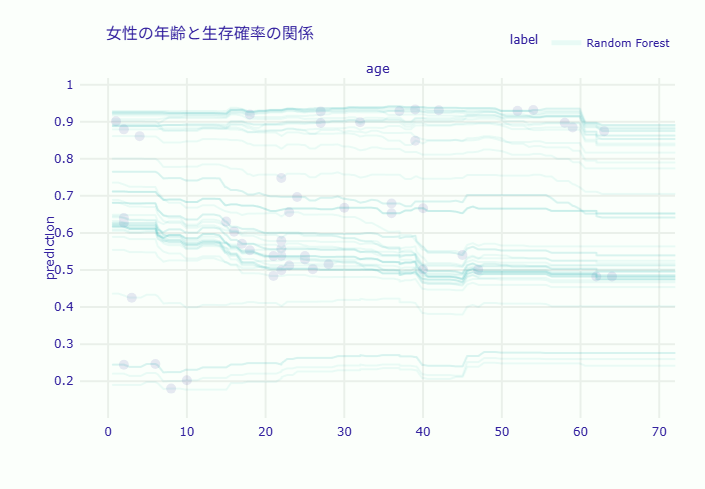
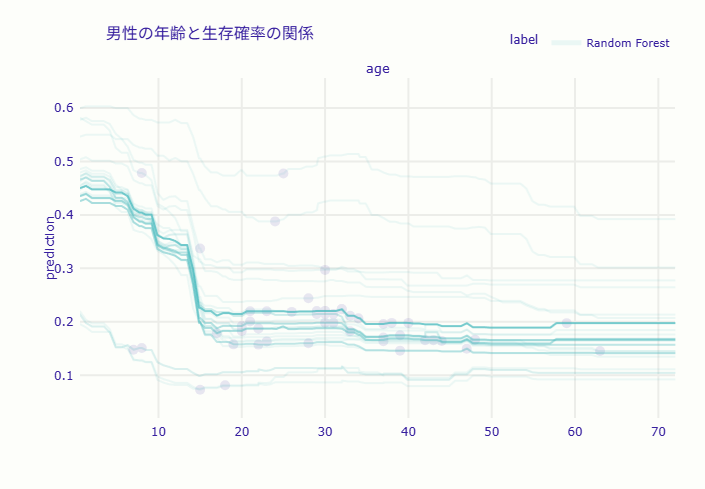
性別ごとのICEプロットを比較すると、興味深いパターンが見えてきます。
女性のICEプロットでは、ほとんどの線が高い位置(生存確率0.5以上)に集中しており、年齢による低下も緩やかです。これは、女性の場合、年齢に関わらず比較的高い生存率を維持することを示しています。
一方、男性のICEプロットでは、線が低い位置(生存確率0.3以下)に集中しており、年齢とともに急激に低下する傾向が見られます。特に高齢の男性では、生存確率がほぼゼロに近づくケースも見られます。
整理すると、次のようなことが分かります。
- 子供(5歳)の場合は性別による差が比較的小さく、「子供優先」の原則が両性に適用されていた
- 成人(20歳、40歳)では性別による差が最大となり、「女性優先」の原則が強く作用していたことが明らか
- 高齢者(60歳)でも女性優先は維持されていますが、両性とも生存率は低い傾向にある
ICEから発見できる重要なインサイト
ICEプロットの分析から、重要な発見があります。
第一に、交互作用の発見です。
年齢の影響は性別によって大きく異なることが明確になりました。これはPDPだけでは見えなかった重要な情報です。
第二に、例外的なパターンの検出です。
一部の高齢者でも高い生存確率を示すケースがあり、これは1等客室の女性乗客である可能性を示唆しています。
第三に、モデルの安定性の確認です。
ICE曲線が滑らかで一貫性があることから、モデルが安定した予測を行っている証拠と言えます。
ALE(Accumulated Local Effects):PDPの進化形
PDPは強力な手法ですが、一つ弱点があります。それは、特徴量間に相関がある場合、誤った解釈を導く可能性があることです。
ここで登場するのがALE(Accumulated Local Effects:累積局所効果)です。
PDPの限界とALEの必要性
タイタニックの例で考えてみましょう。
「運賃(fare)」と「客室クラス(class)」には強い相関があります。1等客室の乗客は高い運賃を払い、3等客室の乗客は低い運賃を払っています。
PDPで運賃の影響を見るとき、「3等客室の乗客が200ドルの運賃を払った場合」という、現実にはありえない組み合わせも計算に含まれてしまいます。
これは、データの分布から外れた領域(外挿領域)での予測を含むため、結果が歪む可能性があります。
ALEは、この問題を条件付き分布を使って解決します。各データポイントの周辺での変化だけを見ることで、現実的な範囲内での影響を測定します。
ALEの仕組みを直感的に理解する
ALEの計算方法は、PDPとは異なるアプローチを取ります。
PDPが「すべてのデータに対して、ある値を強制的に代入して平均を取る」のに対し、ALEは「データを区間ごとに分け、各区間内での変化量を累積する」という方法を使います。
これは、山の高さを測るときに、山全体を一度に測るのではなく、登山道に沿って少しずつ標高差を足し合わせていくようなものです。
DALEXでALEを計算する
DALEXでは、model_profileメソッドのtype引数にaccumulatedを指定することでALEを計算できます。
# 年齢のALEプロットを計算
ale_age = explainer_rf.model_profile(
type='accumulated',
variables=['age']
)
# ALEプロットを表示
ale_age.plot(show=True)
以下、実行結果です。
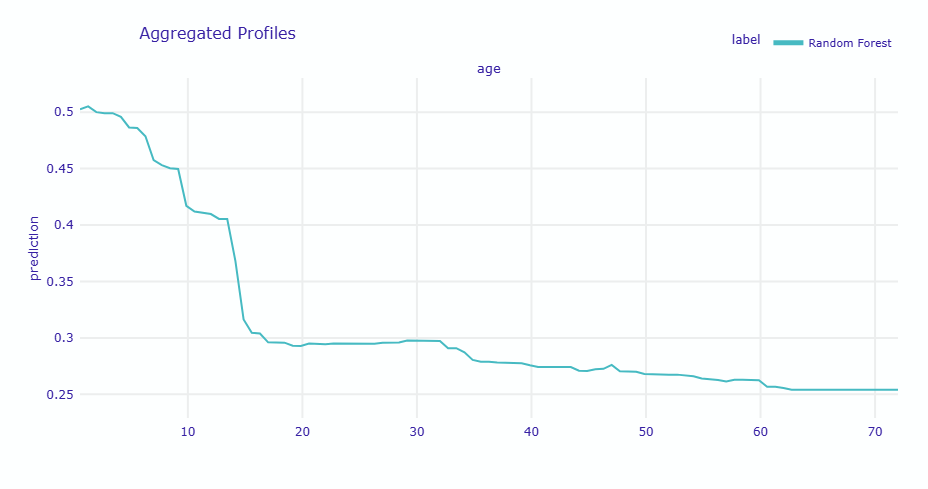
グラフのy軸はPDPと同様に予測値(生存確率)を示しています。ALEでは、特徴量間の相関による歪みを除去した上で、各特徴量の値における予測への影響を表現しています。
両方を同時に計算して、違いを確認してみましょう。
# 複数変数でPDPとALEを計算
variables_to_compare = ['age', 'fare']
# PDPの計算
pdp_compare = explainer_rf.model_profile(
type='pdp',
variables=variables_to_compare
)
# ALEの計算
ale_compare = explainer_rf.model_profile(
type='accumulated',
variables=variables_to_compare
)
# グラフのy軸の最小値と最大値
y_range = [
0,
max(
pdp_compare.result['_yhat_'].max(),
ale_compare.result['_yhat_'].max()
) * 1.1
]
# PDPプロット
fig_pdp = pdp_compare.plot(show=False)
fig_pdp.update_layout(title="PDP")
fig_pdp.update_yaxes(range=y_range)
fig_pdp.show()
# ALEプロット
fig_ale = ale_compare.plot(show=False)
fig_ale.update_layout(title="ALE")
fig_ale.update_yaxes(range=y_range)
fig_ale.show()
以下、実行結果です。
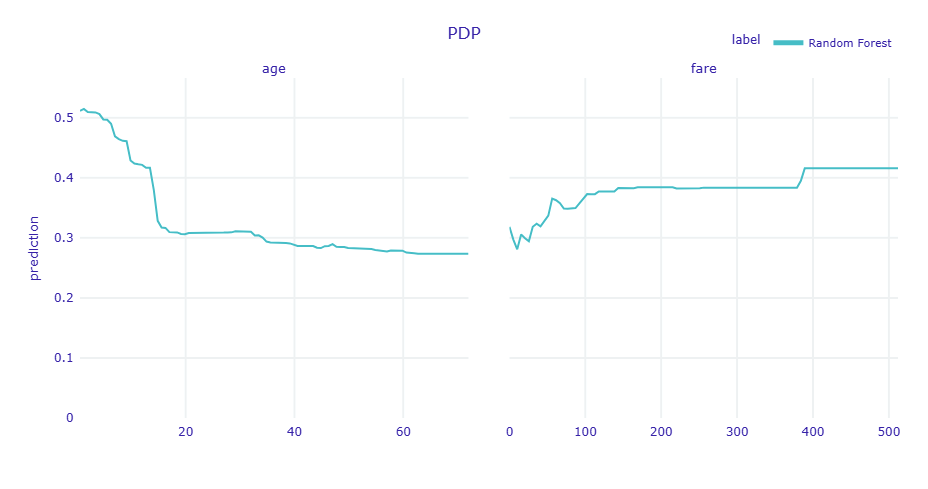
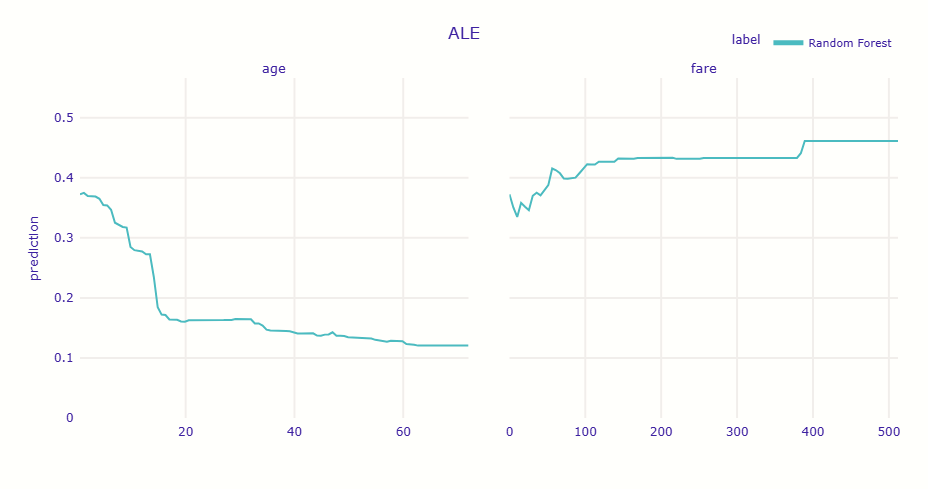
PDPとALEでグラフの形状(傾向)は一致しているものの、数値(生存確率)の水準が異なっていることが分かります。
- PDP(過大評価の傾向): 現実にはあり得ないデータも含めて平均化するため、他の特徴量との相関によるバイアスが入り込み、予測確率が高く(もしくは低く)算出されています。
- ALE(純粋な効果): 現実のデータが存在する範囲内でのみ変化を計算するため、他の特徴量(客室ランクや性別など)の影響を排除し、バイアスのない純粋な効果を示しています。
つまり、変数が複雑に関係し合っている今回のデータでは、ALEの低い数値の方が信頼できる解釈となります。
Surrogate Model:ブラックボックスを透明なモデルで解釈
ここまで紹介した手法は、特定の特徴量の影響を可視化するものでした。
しかし、「そもそもこの複雑なモデルは、全体としてどんなルールで判断しているのか」を知りたいこともあります。
そんなときに使うのがSurrogate Model(代理モデル)です。
代理モデルとは何か
代理モデルの考え方は非常にシンプルです。
複雑なブラックボックスモデルの予測結果を、解釈しやすいモデル(決定木など)で模倣するのです。
これは、外国語の本を日本語に翻訳するようなものです。原著の複雑さは失われるかもしれませんが、内容の概要を理解することができます。
タイタニックの例で言えば、ランダムフォレストの予測結果を、人間が読める決定木で近似します。これにより、「だいたいこういうルールで判断している」という全体像を把握できます。
決定木による代理モデルの構築
ランダムフォレストの予測結果を「正解ラベル」として、決定木を学習させます。
from sklearn.tree import DecisionTreeClassifier
# ランダムフォレストの予測結果を取得
rf_pred = rf_model.predict(X_test)
# 決定木で代理モデルを構築
surrogate_tree = DecisionTreeClassifier(
#max_depth=5,
min_samples_leaf=10,
random_state=42
)
# ランダムフォレストの予測を「正解」として学習
surrogate_tree.fit(X_test, rf_pred)
# 代理モデルの忠実度を確認
fidelity = surrogate_tree.score(X_test, rf_pred)
print(f"忠実度: {fidelity:.2%}")
以下、実行結果です。
忠実度: 96.56%
忠実度(Fidelity)とは、代理モデルが元のブラックボックスモデルの予測をどれだけ再現できているかを示す指標です。
約90%の忠実度があれば、代理モデルは元のモデルの振る舞いをかなりよく捉えていると言えます。
決定木を可視化して、判断ルールを確認します。
plt.figure(figsize=(10, 8))
plot_tree(
surrogate_tree,
feature_names=X.columns.tolist(),
class_names=['死亡', '生存'],
filled=True,
rounded=True,
fontsize=10,
proportion=True
)
plt.title('ランダムフォレストの代理モデル(決定木)', fontsize=14)
plt.tight_layout()
plt.show()
以下、実行結果です。
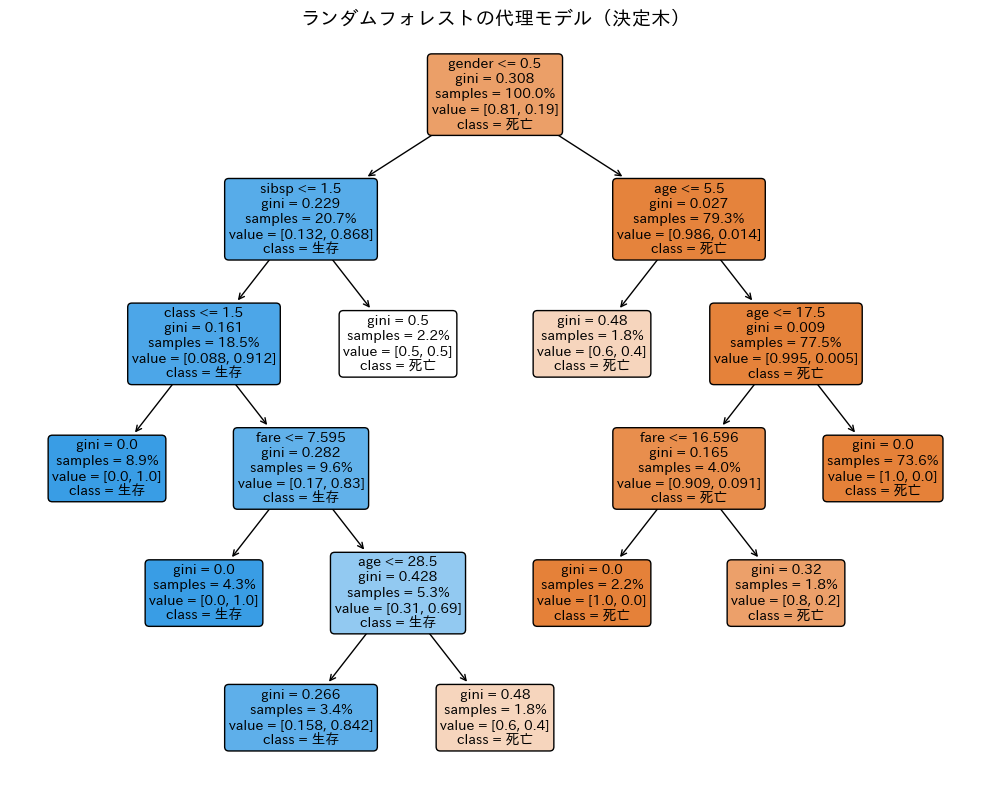
複数モデルの比較:どのモデルを選ぶべきか
実務では、複数のモデルを作成して比較することが重要です。
精度だけでなく、解釈性や安定性も考慮する必要があります。
DALEXの強力な機能の一つは、異なるアルゴリズムで作成したモデルを同じ土俵で比較できることです。
モデル比較の準備
まず、ロジスティック回帰モデルを構築します。ロジスティック回帰は線形モデルの一種で、解釈しやすいという特徴があります。
ランダムフォレストなどのツリー系のアルゴリズムと異なり、カテゴリカル変数(質的変数)は0-1変数(ワンホットエンコーディング)である必要があります。
そのため、get_dummiesでカテゴリカル変数を0-1変数に変換したデータセットで、ロジスティック回帰モデルを構築します。
# ロジスティック回帰モデル用のデータセット準備
# カテゴリ変数(文字データ)を数値に変換
lr_X = pd.get_dummies(titanic.drop('survived', axis=1)) # 説明変数(予測に使う情報)
lr_y = titanic['survived'] # 目的変数(予測したい結果)
# 訓練データとテストデータに分割
lr_X_train, lr_X_test, lr_y_train, lr_y_test = train_test_split(
lr_X, # 説明変数
lr_y, # 目的変数
test_size=0.25, # テストデータの割合
random_state=42
)
# ロジスティック回帰モデルの構築
print("=== ロジスティック回帰モデルの構築 ===")
from sklearn.linear_model import LogisticRegression
lr_model = LogisticRegression(
max_iter=1000, # 収束までの最大反復回数
random_state=42 # 再現性のため
)
# モデルの訓練と評価
lr_model.fit(lr_X_train, lr_y_train)
lr_accuracy = lr_model.score(lr_X_test, lr_y_test)
print(f"テスト精度: {lr_accuracy:.2%}")
# 係数を確認(線形モデルの利点)
print("\n各特徴量の係数:")
for feature, coef in zip(lr_X.columns, lr_model.coef_[0]):
print(f" {feature}: {coef:+.3f}")
以下、実行結果です。
=== ロジスティック回帰モデルの構築 === テスト精度: 77.17% 各特徴量の係数: age: -0.039 fare: +0.001 sibsp: -0.318 parch: -0.043 gender_female: +1.424 gender_male: -1.387 class_1st: +1.220 class_2nd: -0.173 class_3rd: -1.047 class_deck crew: +1.843 class_engineering crew: +0.069 class_restaurant staff: -1.679 class_victualling crew: -0.195 embarked_Belfast: -0.124 embarked_Cherbourg: +0.382 embarked_Queenstown: -0.197 embarked_Southampton: -0.024
係数を見ることで、各特徴量の影響の大きさと方向(正の影響か負の影響か)が一目で分かるのが線形モデルの大きな利点です。
次に、XGBoostモデルを構築します。XGBoostは勾配ブースティングという手法を使った高性能なモデルです。
# XGBoostモデルの構築
print("=== XGBoostモデルの構築 ===")
from xgboost import XGBClassifier
xgb_model = XGBClassifier(
n_estimators=100, # 木の数
max_depth=5, # 各決定木の最大深さ
random_state=42, # 再現性のため
eval_metric='logloss' # 評価指標を修正
)
# モデルの訓練と評価
xgb_model.fit(X_train, y_train)
xgb_accuracy = xgb_model.score(X_test, y_test)
print(f"テスト精度: {xgb_accuracy:.2%}")
以下、実行結果です。
=== XGBoostモデルの構築 === テスト精度: 78.99%
ランダムフォレストのモデルは既にあるので構築しません。
3つのモデルの精度を比較します。
# 3つのモデルの精度を比較
print("=== モデル精度の比較 ===")
print(f"ランダムフォレスト: {test_accuracy:.2%}")
print(f"ロジスティック回帰: {lr_accuracy:.2%}")
print(f"XGBoost: {xgb_accuracy:.2%}")
以下、実行結果です。
=== モデル精度の比較 === ランダムフォレスト: 79.53% ロジスティック回帰: 77.17% XGBoost: 78.99%
3つのモデルの精度を比較すると、ランダムフォレストとXGBoostが高い精度を示していることが分かります。
精度だけでモデルを選ぶべきでしょうか?
各モデルのExplainerを作成して、解釈の準備をします。ランダムフォレストのExplainerは既にあるので作成しません。
# ロジスティック回帰のExplainer
explainer_lr = dx.Explainer(# ロジスティック回帰のExplainer
explainer_lr = dx.Explainer(
lr_model, lr_X_test, lr_y_test,
label="Logistic Regression"
)
# XGBoostのExplainer
explainer_xgb = dx.Explainer(
xgb_model, X_test, y_test,
label="XGBoost"
)
以下、実行結果です。
Preparation of a new explainer is initiated -> data : 552 rows 17 cols -> target variable : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray. -> target variable : 552 values -> model_class : sklearn.linear_model._logistic.LogisticRegression (default) -> label : Logistic Regression -> predict function : <function yhat_proba_default at 0x7f26c6ee8c20> will be used (default) -> predict function : Accepts pandas.DataFrame and numpy.ndarray. -> predicted values : min = 0.0178, mean = 0.327, max = 0.976 -> model type : classification will be used (default) -> residual function : difference between y and yhat (default) -> residuals : min = -0.973, mean = -0.00829, max = 0.946 -> model_info : package sklearn A new explainer has been created! Preparation of a new explainer is initiated -> data : 552 rows 7 cols -> target variable : Parameter 'y' was a pandas.Series. Converted to a numpy.ndarray. -> target variable : 552 values -> model_class : xgboost.sklearn.XGBClassifier (default) -> label : XGBoost -> predict function : <function yhat_proba_default at 0x7f26c6ee8c20> will be used (default) -> predict function : Accepts pandas.DataFrame and numpy.ndarray. -> predicted values : min = 0.0013, mean = 0.313, max = 1.0 -> model type : classification will be used (default) -> residual function : difference between y and yhat (default) -> residuals : min = -0.986, mean = 0.00925, max = 0.988 -> model_info : package xgboost A new explainer has been created!
特徴量重要度の比較
各モデルの特徴量重要度を計算して比較します。
# ランダムフォレストの変数重要度 vi_rf = explainer_rf.model_parts() # ロジスティック回帰の変数重要度 vi_lr = explainer_lr.model_parts() # XGBoostの変数重要度 vi_xgb = explainer_xgb.model_parts() # グラフで比較 vi_rf.plot([vi_lr, vi_xgb], show=True)
以下、実行結果です。
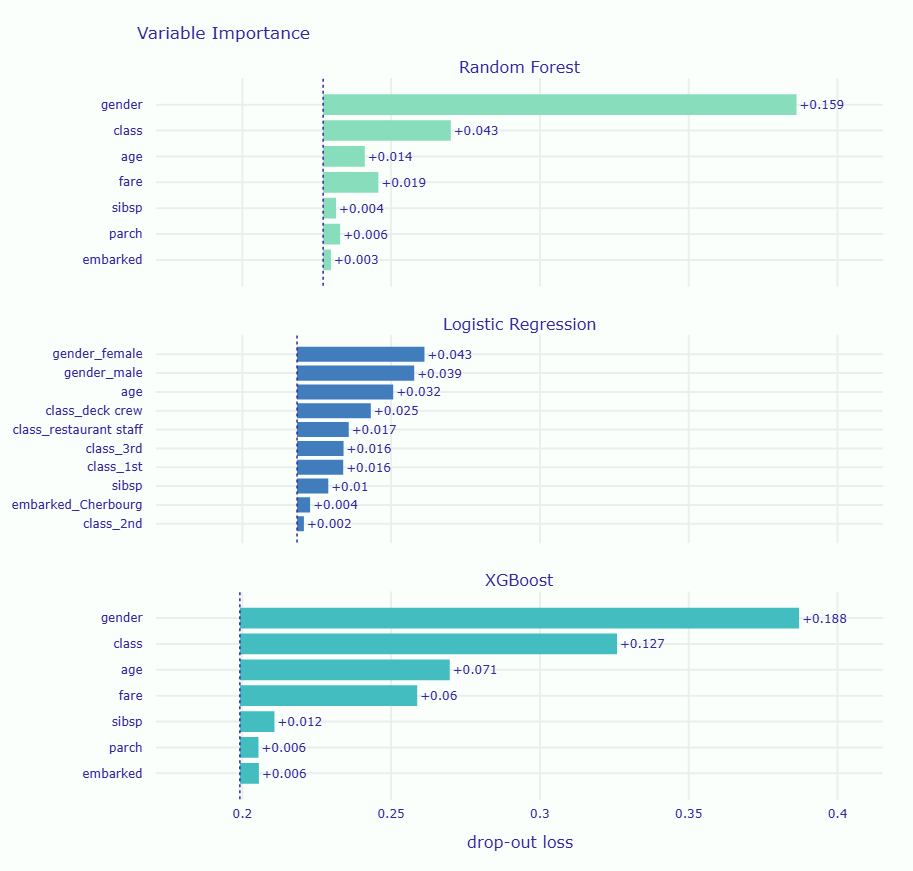
グラフを見ると、どのモデルも性別を最重要視していることが分かります。
これは、異なるアルゴリズムでも同じパターンを捉えていることを示しており、この発見の信頼性を高めます。
PDPによる詳細比較
年齢の影響を3モデルで比較してみましょう。
# 年齢のPDPを3モデルで比較
# ランダムフォレストのPDP
pdp_rf_age = explainer_rf.model_profile(type='pdp', variables=['age'])
# ロジスティック回帰のPDP
pdp_lr_age = explainer_lr.model_profile(type='pdp', variables=['age'])
# XGBoostのPDP
pdp_xgb_age = explainer_xgb.model_profile(type='pdp', variables=['age'])
# 特定の年齢での予測値を比較
print("\n20歳と60歳での予測値比較:")
for age in [20, 60]:
# RF: 段階フィルタで AND 相当
rf_df = pdp_rf_age.result.copy()
rf_df = rf_df[rf_df['_vname_'] == 'age']
rf_df = rf_df[rf_df['_x_'].round() == age]
rf_pred = rf_df['_yhat_'].mean() if not rf_df.empty else float('nan')
# LR
lr_df = pdp_lr_age.result.copy()
lr_df = lr_df[lr_df['_vname_'] == 'age']
lr_df = lr_df[lr_df['_x_'].round() == age]
lr_pred = lr_df['_yhat_'].mean() if not lr_df.empty else float('nan')
# XGB
xgb_df = pdp_xgb_age.result.copy()
xgb_df = xgb_df[xgb_df['_vname_'] == 'age']
xgb_df = xgb_df[xgb_df['_x_'].round() == age]
xgb_pred = xgb_df['_yhat_'].mean() if not xgb_df.empty else float('nan')
print(f"\n{age}歳:")
print(f" ランダムフォレスト: {rf_pred:.3f}")
print(f" ロジスティック回帰: {lr_pred:.3f}")
print(f" XGBoost: {xgb_pred:.3f}")
# グラフで比較
pdp_rf_age.plot(
[pdp_lr_age, pdp_xgb_age], # 追加のPDPをリストで指定
geom='profiles', # プロファイルをプロット
variables=['age'], # 変数を指定
show=True # グラフを表示
)
以下、実行結果です。
Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 9.31it/s] Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 195.43it/s] Calculating ceteris paribus: 100%|██████████| 1/1 [00:00<00:00, 50.00it/s] 20歳と60歳での予測値比較: 20歳: ランダムフォレスト: 0.306 ロジスティック回帰: 0.381 XGBoost: 0.328 60歳: ランダムフォレスト: 0.275 ロジスティック回帰: 0.177 XGBoost: 0.175
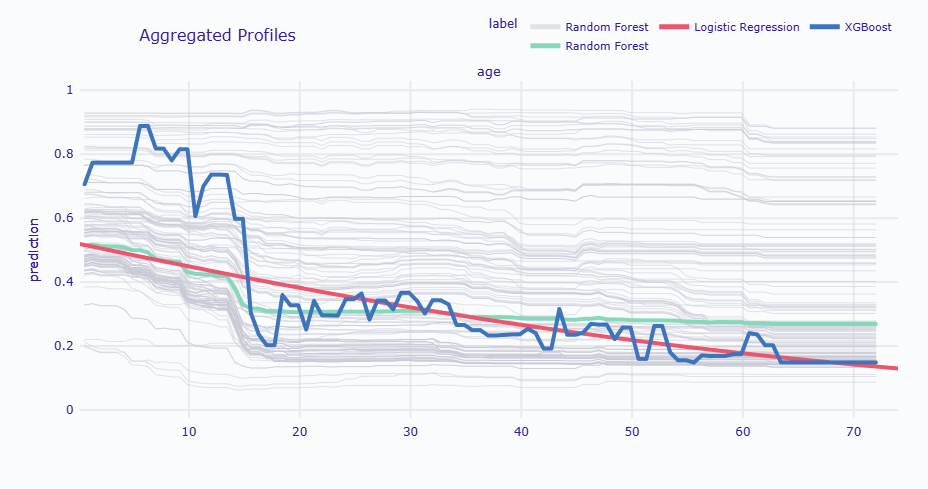
PDPの比較から、各モデルの特性が明確に見えてきます。
ロジスティック回帰は滑らかな直線的な関係を示し、最もシンプルで解釈しやすいパターンです。
ランダムフォレストは階段状ですが妥当な曲線を描いており、現実的なパターンを捉えています。
XGBoostは細かい変動があり、訓練データの細かいパターンまで学習している可能性があります。これは過学習のリスクを示唆しています。
モデル選択の判断基準
モデル選択においては、幾つかの観点から総合的に判断する必要があります。
精度の観点では、XGBoostやランダムフォレストが高く、ロジスティック回帰が低いです。しかし、精度だけがすべてではありません。
解釈性の観点では、ロジスティック回帰が最も優れています。係数を見るだけで各変数の影響が分かり、説明が簡単です。ランダムフォレストは中程度の解釈性を持ち、XGBoostは最も解釈が困難です。
安定性の観点でも、ロジスティック回帰が最も安定しており、新しいデータに対しても一貫した予測を行います。XGBoostは細かいパターンを学習しすぎるため、新しいデータで性能が低下する可能性があります。
したがって、説明責任が重要な場合(医療・金融など)はロジスティック回帰を、バランスを重視する場合(一般的なビジネス利用)はランダムフォレストを、精度最優先の場合はXGBoost(ただし過学習に注意)を選ぶことが推奨されます。
まとめ
今回は、グローバル解釈の主要な手法について、実際のタイタニックデータを使って紹介しました。
PFIにより、性別、客室クラス、年齢が生存の重要な要因であることを発見しました。これらは歴史的事実と一致しており、モデルが適切にパターンを学習していることが確認できました。
PDPを通じて、各特徴量が生存率にどのように影響するかを視覚的に理解しました。年齢が上がるにつれて生存率が低下すること、運賃が高いほど生存率が上がることなど、具体的な関係性を把握できました。
ICEプロットにより、平均に隠された個体差を発見しました。特に、性別による年齢の影響の違いという重要な交互作用を見つけることができました。
ALEを通じて、特徴量間に相関がある場合でも正確な影響を把握する方法を学びました。PDPが現実にはありえない特徴量の組み合わせも計算に含めてしまう問題を、ALEがどのように解決するかを確認しました。
Surrogate Modelにより、複雑なブラックボックスモデルの判断ロジック全体を、人間が読める決定木として近似する方法を紹介しました。「女性と子供を優先、社会階層も考慮」という判断ルールが、明示的なルールとして確認できました。
これらの分析から、タイタニック号の悲劇における社会的な側面が浮き彫りになりました。「女性と子供を優先」という方針、客室クラスによる避難の不平等、これらは単なる統計的パターンではなく、実際の人々の生死を分けた要因でした。
グローバル解釈は、AIモデルの判断根拠を理解し、その妥当性を検証し、必要に応じて改善するための重要な手段です。モデルが現実世界の知識と整合しているか、偏りはないか、これらを確認することで、信頼できるAIシステムを構築できるのです。
次回は、個別の予測に対する説明手法(ローカル解釈)を学びます。
「なぜこの特定の乗客は生存/死亡と予測されたのか」を、SHAPやBreak Downといった手法で詳細に説明する方法を身につけていきましょう。
実際のビジネスシーンでは、全体的な傾向(グローバル解釈)と個別の説明(ローカル解釈)の両方が必要です。ちなみに、今回紹介したICEは厳密にはローカル解釈手法です。PDPとの関係が深いため、今回扱いました。
今回学んだ手法を、ぜひ自分のデータでも試してみてください。データの背後にある物語を読み解く力は、これからのAI時代において必須のスキルとなるでしょう。
DALEXで実践する説明可能AI超入門— 第4回 —ローカル解釈(SHAP/Break Down/Ceteris Paribus)で個別予測を説明する

