Pythonで始める分類モデル入門
— 第2回 —
データの「形」から分ける — 線形判別分析（LDA）入門

124
Pythonで始める分類モデル入門— 第2回 —データの「形」から分ける — 線形判別分析（LDA）入門

こんにちは！「Pythonで始める分類モデル入門」の第2回です。

前回はロジスティック回帰を学び、「確率を直接モデル化する」アプローチで分類問題を解きました。

Pythonで始める分類モデル入門— 第1回 —分類問題ってなに？ ロジスティック回帰で「合格予測」を作ろう

今回は、それとは全く異なる発想の線形判別分析（LDA: Linear Discriminant Analysis）を学びます。

身体測定データから性別を判別する例を通じて、「データの分布」に注目する考え方を理解しましょう。

2つのアプローチ：直接派 vs 分布派

分類問題を解くアプローチは、大きく2つに分かれます。

直接派（識別的アプローチ）は、「与えられたデータに対して、AとBのどちらに属するか（条件付き確率）を直接モデル化する」方法です。

前回学んだロジスティック回帰がこれにあたります。

分布派（生成的アプローチ）は、「Aグループのデータはどのような分布をしているか」「Bグループはどのような分布か」をそれぞれ推定し、新しいデータがどちらの分布から生成されたと考えるのが自然か（＝尤度が高いか）で判断します

今回学ぶLDAがこちらです。

身近な例えで考えてみましょう。あなたが道で犬を見かけたとき、「これは柴犬かゴールデンレトリバーか」を判断するとします。

直接派は、「茶色で小さいから柴犬っぽさ80%」のように、特徴から直接確率を出します。

一方、分布派は、「柴犬は平均体高40cm・体重10kg程度」「ゴールデンレトリバーは平均体高55cm・体重30kg程度」といった知識をもとに、目の前の犬がどちらの典型的な分布に近いかで判断します。実際には個体差があるため、平均値だけでなく分布全体を考えます。

どちらが正しいということはなく、データの性質や目的に応じて使い分けます。

 

準備：必要なライブラリを読み込もう

今回使うライブラリを読み込みます。LDAはscikit-learnのdiscriminant_analysisモジュールに含まれています。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib

# LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
# ロジスティック回帰
from sklearn.linear_model import LogisticRegression

from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 乱数のシードを固定
np.random.seed(42)

 

今回はLDAとロジスティック回帰を比較するので、両方をインポートしています。

 

身体測定データを作ってみよう

今回は「身長と体重から性別を判別する」問題に取り組みます。まずはサンプルデータを作成しましょう。

以下、コードです。

# 男女それぞれ50人分のデータを生成
n_each = 50

# 男性データ（平均：身長170cm, 体重65kg）
male_height = np.random.normal(170, 6, n_each)
male_weight = np.random.normal(65, 8, n_each)

# 女性データ（平均：身長158cm, 体重52kg）
female_height = np.random.normal(158, 5, n_each)
female_weight = np.random.normal(52, 6, n_each)

# DataFrameにまとめる
body_df = pd.DataFrame({
    'height': np.concatenate([male_height, female_height]),
    'weight': np.concatenate([male_weight, female_weight]),
    'gender': ['Male'] * n_each + ['Female'] * n_each
})

print(f"データ数: {len(body_df)}人（男性{n_each}人、女性{n_each}人）")
print(body_df.head())

 

以下、実行結果です。

データ数: 100人（男性50人、女性50人）
       height     weight gender
0  172.980285  67.592672   Male
1  169.170414  61.919342   Male
2  173.886131  59.584624   Male
3  179.138179  69.893410   Male
4  168.595080  73.247996   Male

 

男性は平均身長170cm・体重65kg、女性は平均身長158cm・体重52kgという設定でデータを生成しました。

np.random.normal()は正規分布に従う乱数を生成する関数で、第1引数が平均、第2引数が標準偏差です。

 

データの分布を可視化しよう

LDAは「各グループのデータ分布」を重視する手法です。まずは散布図でデータの分布を確認してみましょう。

以下、コードです。

plt.figure(figsize=(10, 7))

# 男性と女性を別々の色でプロット
for gender, color, marker in [('Male', '#2E86AB', 'o'), ('Female', '#E94F37', 's')]:
    subset = body_df[body_df['gender'] == gender]
    plt.scatter(subset['height'], subset['weight'], 
                c=color, marker=marker, s=80, alpha=0.6, label=gender)

plt.xlabel('Height (cm)', fontsize=12)
plt.ylabel('Weight (kg)', fontsize=12)
plt.title('Height and Weight Distribution by Gender', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

 

以下、実行結果です。

 

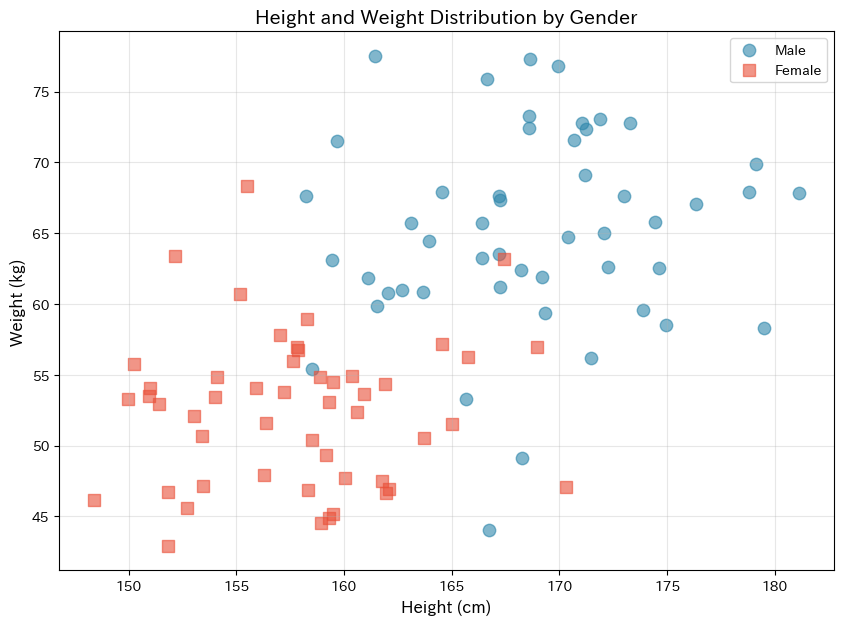
散布図を見ると、男性グループ（青い丸）と女性グループ（赤い四角）がそれぞれ「かたまり」を形成していることがわかります。

完全には分離していませんが、ある程度の傾向は見て取れますね。LDAはこの「かたまりの形」を数学的に捉えて分類を行います。

 

LDAの基本的な考え方

ここからLDAの数学的な仕組みを詳しく見ていきましょう。

　ステップ1：各クラスの分布をモデル化する

LDAは、各クラスのデータが多変量正規分布に従うと仮定します。

2クラス分類（クラス0とクラス1）の場合、各クラスのデータは次の正規分布に従うとします。
$$
\mathbf{x} | Y = k \sim \mathcal{N}(\boldsymbol{\mu}_k, \boldsymbol{\Sigma})
$$

この式は、「クラスが k であると分かっているとき、特徴量ベクトル \mathbf{x} は、平均 \boldsymbol{\mu}_k、共分散行列 \boldsymbol{\Sigma} をもつ多変量正規分布に従う」ということを意味しています。

記号の意味を順に見ていきましょう。

  • \mathbf{x} は、観測されたデータ（特徴量ベクトル）を表します。
  • Y = k は、「データがクラス k に属している」という条件を表します。
  • 記号「\mid」は「〜という条件のもとで」を意味します。
  • 記号「\sim」は「〜に従う」「〜という分布に従って生成される」と読みます。
  • \mathcal{N}(\boldsymbol{\mu}_k, \boldsymbol{\Sigma}) は、平均が \boldsymbol{\mu}_k、共分散が \boldsymbol{\Sigma} の多変量正規分布を表します。

つまりこの式は、「クラスごとに、データの分布の中心（平均）は異なるが、ばらつき方（共分散）は共通である」というLDAの重要な仮定を、1行の数式で表しているのです。

つまり、データの「ばらつき方」は男女で同じだと仮定しています。この仮定があるから、LDAの判別境界が「直線」になるのです。

 

　ステップ2：ベイズの定理で事後確率を計算する

新しいデータ \mathbf{x} が与えられたとき、それがクラス k に属する確率（事後確率）を求めたいです。

ここで、次のようなベイズの定理が登場します。
$$
P(Y = k | \mathbf{x}) = \frac{P(\mathbf{x} | Y = k) \cdot P(Y = k)}{P(\mathbf{x})}
$$

P(Y = k | \mathbf{x}) は事後確率で、データ \mathbf{x} が与えられたときにクラス k である確率です。これが私たちの知りたいものです。

右辺の各項の意味を確認しましょう。

  • P(\mathbf{x} | Y = k) は尤度で、クラス k のデータから \mathbf{x} が生成される確率です
  • P(Y = k) は事前確率で、クラス k がどれくらいの割合で出現するかです
  • P(\mathbf{x}) は周辺尤度で、すべてのクラスを通じて \mathbf{x} が観測される確率です

 

　ステップ3：判別関数を導出する

2クラス分類では、P(Y = 1 | \mathbf{x}) と P(Y = 0 | \mathbf{x}) を比較して、大きい方のクラスに分類します。

ステップ2のベイズの定理の右辺の分母 \(P(\mathbf{x})\) は両方で共通なので、比較には影響しません。そのため、分子である \(P(\mathbf{x} | Y = k) \cdot P(Y = k)\) の大きさを比較すれば十分です。

分子に含まれる多変量正規分布の確率密度関数 \(P(\mathbf{x} | Y = k)\) は次のように書けます。
$$
P(\mathbf{x} | Y = k) = \frac{1}{(2\pi)^{p/2}|\boldsymbol{\Sigma}|^{1/2}} \exp\left(-\frac{1}{2}(\mathbf{x} – \boldsymbol{\mu}_k)^T \boldsymbol{\Sigma}^{-1} (\mathbf{x} – \boldsymbol{\mu}_k)\right)
$$

ここで p は特徴量の次元数です。

この積の形を扱いやすくするため、対数を取って分子を整理していくと、以下のような 判別関数 \(\delta_k(\mathbf{x})\) が得られます。
$$
\delta_k(\mathbf{x}) = \mathbf{x}^T \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_k – \frac{1}{2}\boldsymbol{\mu}_k^T \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_k + \log(\pi_k)
$$

ここで \pi_k = P(Y = k) は事前確率です。

LDAでは、事後確率の大小を直接比較する代わりに、この判別関数 \delta_k(\mathbf{x}) を用い、その値が最大となるクラスに分類します。

 

　ステップ4：クラス分類する

新しいデータ \mathbf{x} が与えられたら、ステップ3で導出した判別関数\delta_k(\mathbf{x}) を各クラスについて計算します。

そして、判別関数の値が最も大きいクラスにデータを分類します。これは、事後確率 P(Y = k \mid \mathbf{x}) が最も大きいクラスを選んでいることと等価です。

LDAでは、この分類結果とあわせて、「どれくらい確信を持って判定したか」を表す指標も得ることができます。

具体的には、各クラスの事後確率 P(Y = k \mid \mathbf{x}) を計算し、 最も確率が高いクラスの事後確率を、その予測の確信度として解釈します。

たとえば……

  • あるクラスの事後確率が 99% の場合 → そのクラスに強く偏っており、モデルは高い確信を持って判定しています
  • 事後確率が 50%前後 の場合 → どちらのクラスとも言い切れず、判定は微妙です

このように、確信度は分類結果がどれくらい「境界から離れているか」を表す量だと考えることができます。

数式の観点では、これはクラス間の判別関数 \delta_k(\mathbf{x}) の値がどれだけ離れているかに対応しています。

  • 判別関数の値に大きな差がある → 事後確率にも大きな差が生じ、確信度は高くなる
  • 判別関数の値がほぼ等しい → 境界付近のデータで、確信度は低くなる

なお、ここでいう確信度は、 LDAが仮定した確率モデルにもとづく相対的な指標です。

「必ず正しい確率」や「人間の主観的な自信」を表すものではなく、あくまで「このモデルの仮定のもとでは、どれくらい一方のクラスらしいか」を数値化したものだという点に注意しましょう。

 

　判別境界は直線になる

クラス0とクラス1の判別境界は、\delta_1(\mathbf{x}) = \delta_0(\mathbf{x}) となる点の集合です。

判別関数の式を見ると、\mathbf{x} について1次式（線形）であることがわかります。

これを整理すると、判別境界は次の形になります。

$$
\mathbf{w}^T \mathbf{x} + b = 0
$$

ここで、\mathbf{w} = \boldsymbol{\Sigma}^{-1}(\boldsymbol{\mu}_1 - \boldsymbol{\mu}_0) は境界線の法線ベクトル、b は定数項です。

これはまさに直線（2次元の場合）や平面（3次元の場合）の方程式です。

共分散行列がクラス間で共通という仮定があるからこそ、\mathbf{x} の2次の項が消えて、境界が線形になるのです。

もし共分散行列がクラスごとに異なると仮定すると、境界は曲線になります（これを二次判別分析, QDAと呼びます）。

 

　数式のまとめ

数式が多くて混乱したかもしれないので、LDAが実際に行っていることを整理しましょう。

まず訓練時には、各クラスの平均ベクトル \boldsymbol{\mu}_k を計算し、全データから共通の共分散行列 \boldsymbol{\Sigma} を計算し、各クラスの事前確率 \pi_k（通常はデータ中の割合）を計算します。

次に予測時には、新しいデータ \mathbf{x} に対して各クラスの判別関数 \delta_k(\mathbf{x}) を計算し、最も値が大きいクラスに分類します。

 

各グループの「中心」を確認しよう

数式で見た \boldsymbol{\mu}_k（平均ベクトル）を、実際のデータから計算してみましょう。

以下、コードです。

# グループごとの平均を計算
group_means = body_df.groupby('gender')[
    ['height', 'weight']
].mean()

print("【各グループの平均値 μ_k】")
print(group_means)
print()

# 全体の平均も確認
overall_mean = body_df[['height', 'weight']].mean()
print("【全体の平均値】")
print(
    f"身長: {overall_mean['height']:.1f}cm,"
    f"体重: {overall_mean['weight']:.1f}kg"
)

 

以下、実行結果です。

【各グループの平均値 μ_k】
            height     weight
gender                       
Female    157.803562  52.503380
Male      168.647157  65.142247

【全体の平均値】
身長: 163.2cm,体重: 58.8kg

 

これがLDAで使われる各クラスの平均ベクトル \boldsymbol{\mu}_k です。

LDAは新しいデータとこれらの平均との「距離」を計算しますが、単純なユークリッド距離ではなく、共分散行列を考慮したマハラノビス距離を使います。

 

共分散行列を確認しよう

LDAのもう一つの重要な要素、共分散行列 \boldsymbol{\Sigma} も見てみましょう。

共分散行列は、変数間の関係性（一方が増えるともう一方も増える、など）を表します。

以下、コードです。

# 特徴量を取り出す
X = body_df[['height', 'weight']].values
y = (body_df['gender'] == 'Male').astype(int).values

# 全体の共分散行列を計算（LDAでは共通の共分散を仮定）
cov_matrix = np.cov(X.T)

print("【共分散行列 Σ】")
print(cov_matrix)
print()
print(f"身長の分散: {cov_matrix[0,0]:.2f}")
print(f"体重の分散: {cov_matrix[1,1]:.2f}")
print(f"身長と体重の共分散: {cov_matrix[0,1]:.2f}")

 

以下、実行結果です。

【共分散行列 Σ】
[[57.98371285 37.47350101]
 [37.47350101 78.7855376 ]]

身長の分散: 57.98
体重の分散: 78.79
身長と体重の共分散: 37.47

 

共分散行列の対角成分は各変数の分散（ばらつきの大きさ）、非対角成分は変数間の共分散（一緒に変動する度合い）を表します。

正の共分散は「身長が高い人は体重も重い傾向がある」ことを意味します。

 

scikit-learnでLDAを実装しよう

それでは実際にLDAモデルを作成してみましょう。

scikit-learnを使えば、ロジスティック回帰と同じくらい簡単に実装できます。

以下、コードです。

# LDAモデルを作成して訓練
lda_model = LinearDiscriminantAnalysis()
lda_model.fit(X, y)

print("【LDAモデルの学習結果】")
print(
    f"女性グループの平均 μ_0: "
    f"身長={lda_model.means_[0, 0]:.1f}cm, " 
    f"体重={lda_model.means_[0, 1]:.1f}kg"
)
print(
    f"男性グループの平均 μ_1: "
    f"身長={lda_model.means_[1, 0]:.1f}cm, "
    f"体重={lda_model.means_[1, 1]:.1f}kg"
)
print(f"事前確率 π_0 (女性): {lda_model.priors_[0]:.2f}")
print(f"事前確率 π_1 (男性): {lda_model.priors_[1]:.2f}")

 

以下、実行結果です。

【LDAモデルの学習結果】
女性グループの平均 μ_0: 身長=157.8cm, 体重=52.5kg
男性グループの平均 μ_1: 身長=168.6cm, 体重=65.1kg
事前確率 π_0 (女性): 0.50
事前確率 π_1 (男性): 0.50

 

LDAモデルが訓練できました。

lda_model.means_には各クラスの平均ベクトル、lda_model.priors_には事前確率が格納されています。

事前確率は、訓練データ中の各クラスの割合から自動的に計算されます（今回は男女50人ずつなので、どちらも0.5）。

 

判別境界を可視化しよう

LDAがどのような境界線でデータを分けているか、可視化してみましょう。

境界線を描くために、グリッド上の各点でどちらのクラスに分類されるかを計算します。

以下、コードです。

# メッシュグリッドを作成（判別領域を塗り分けるため）
h = 0.5  # グリッドの細かさ
x_min, x_max = X[:, 0].min() - 5, X[:, 0].max() + 5
y_min, y_max = X[:, 1].min() - 5, X[:, 1].max() + 5
xx, yy = np.meshgrid(
    np.arange(x_min, x_max, h), 
    np.arange(y_min, y_max, h)
)

# グリッド上の各点を予測
Z = lda_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 判別領域とデータ点をプロット
plt.figure(figsize=(10, 7))
plt.contourf(xx, yy, Z, alpha=0.3, cmap='RdBu')
plt.scatter(
    X[y==0, 0], X[y==0, 1], 
    c='#E94F37', s=80, alpha=0.7, 
    label='Female'
)
plt.scatter(
    X[y==1, 0], X[y==1, 1], 
    c='#2E86AB', s=80, alpha=0.7, 
    label='Male'
)
plt.xlabel('Height (cm)')
plt.ylabel('Weight (kg)')
plt.title('LDA Decision Boundary')
plt.legend()
plt.show()

 

以下、実行結果です。

 

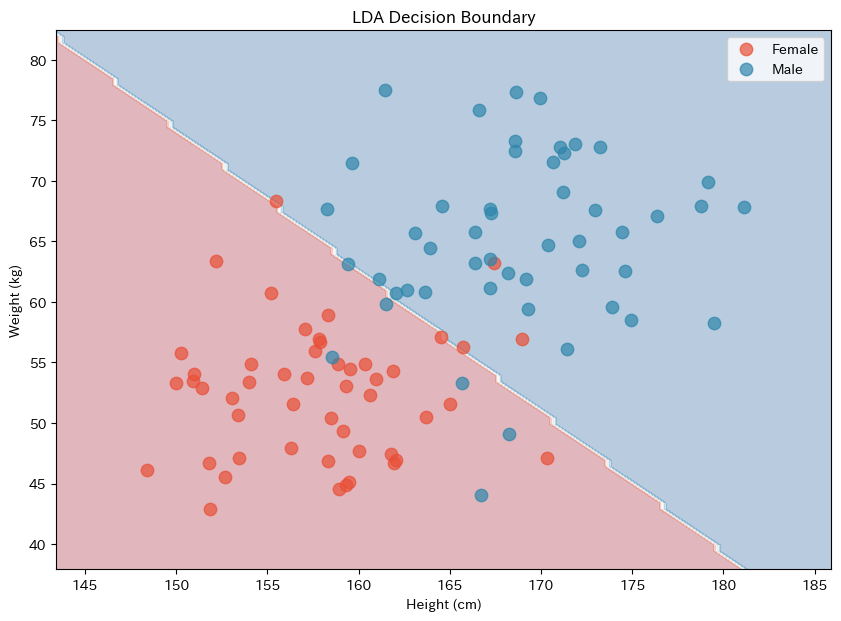
背景色が分類領域を表しています。

青い領域は「男性」と予測される領域、赤い領域は「女性」と予測される領域です。

境界線は直線になっていますね。これは先ほど数式で確認した通り、共分散行列が共通という仮定から導かれる結果です。

 

新しいデータを予測してみよう

訓練したモデルを使って、新しいデータの性別を予測してみましょう。

LDAも確率を出力できるので、「どれくらい確信を持って判定したか」がわかります。

以下、コードです。

# 予測したい人のデータ
new_persons = [
    [165, 55],  # 身長165cm, 体重55kg
    [175, 70],  # 身長175cm, 体重70kg
    [162, 60],  # 身長162cm, 体重60kg（境界付近）
]

print("【新しいデータの予測結果】")
print("-" * 55)

for height, weight in new_persons:
    pred = lda_model.predict([[height, weight]])[0]
    prob = lda_model.predict_proba([[height, weight]])[0]
    gender = "Male" if pred == 1 else "Female"
    confidence = max(prob) * 100
    
    print(
        f"身長{height}cm, 体重{weight}kg → "
        f"{gender}（確信度: {confidence:.1f}%）"
    )

 

以下、実行結果です。

【新しいデータの予測結果】
-------------------------------------------------------
身長165cm, 体重55kg → Female（確信度: 62.8%）
身長175cm, 体重70kg → Male（確信度: 99.9%）
身長162cm, 体重60kg → Female（確信度: 51.9%）

 

確信度が50%に近い場合は、境界線付近のデータで判定が微妙であることを示しています。

数式で見た判別関数 \delta_k(\mathbf{x}) の値がほぼ等しいとき、このような状況が起こります。

 

ロジスティック回帰と比較してみよう

同じデータに対して、前回学んだロジスティック回帰も適用し、LDAと比較してみましょう。

以下、コードです。

# ロジスティック回帰モデルを作成して訓練
lr_model = LogisticRegression(random_state=42)
lr_model.fit(X, y)

# 両モデルの精度を比較
lda_accuracy = accuracy_score(y, lda_model.predict(X))
lr_accuracy = accuracy_score(y, lr_model.predict(X))

print("【モデル精度の比較】")
print(f"LDA（線形判別分析）: {lda_accuracy*100:.1f}%")
print(f"ロジスティック回帰:  {lr_accuracy*100:.1f}%")

 

以下、実行結果です。

【モデル精度の比較】
LDA（線形判別分析）: 90.0%
ロジスティック回帰:  91.0%

 

多くの場合、両者の精度は非常に似ています。

これは、どちらも「線形の境界線」でデータを分ける手法だからです。

しかし、アプローチが異なるため、データの特性によっては差が出ることもあります。

 

判別境界を並べて比較しよう

2つの手法の判別境界を並べて表示してみましょう。

以下、コードです。

fig, axes = plt.subplots(2, 1, figsize=(8, 12))

models = [
    ('LDA', lda_model), 
    ('Logistic Regression', lr_model)
]

for ax, (name, model) in zip(axes, models):
    # 判別領域を計算
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # プロット
    ax.contourf(xx, yy, Z, alpha=0.3, cmap='RdBu')
    ax.scatter(
        X[y==0, 0], X[y==0, 1], 
        c='#E94F37', s=60, alpha=0.7, 
        label='Female'
    )
    ax.scatter(
        X[y==1, 0], X[y==1, 1], 
        c='#2E86AB', s=60, alpha=0.7, 
        label='Male'
    )
    ax.set_xlabel('Height (cm)')
    ax.set_ylabel('Weight (kg)')
    ax.set_title(name)
    ax.legend()

plt.tight_layout()
plt.show()

 

以下、実行結果です。

 

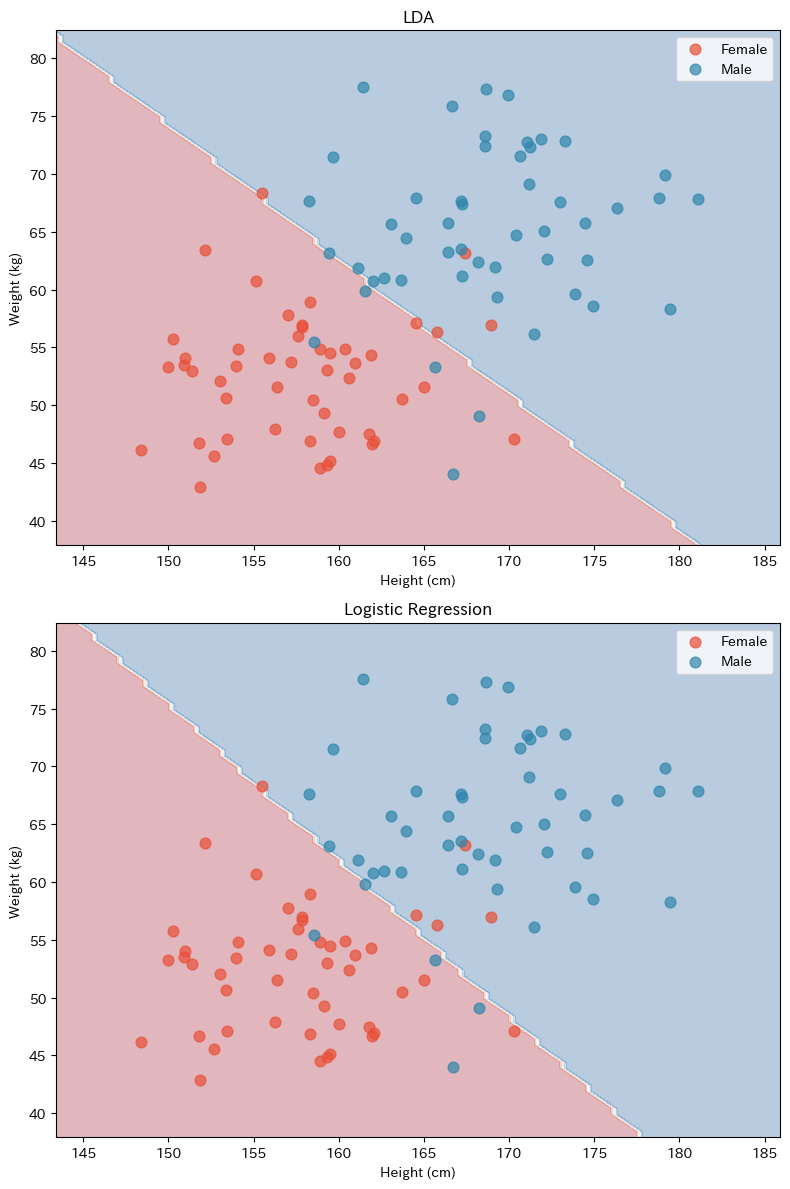
2つの判別境界はほぼ同じ位置にありますが、微妙に傾きが異なることがあります。

これは、LDAが「データの分布形状（正規分布を仮定）」を考慮しているのに対し、ロジスティック回帰は「確率を最大化する境界」を直接求めているという違いによるものです。

 

LDAとロジスティック回帰、どう使い分ける？

LDAとロジスティック回帰は、どちらも分類問題でよく使われる手法ですが、「確率をどう考えるか」という点でアプローチが異なります。

　ロジスティック回帰の復習

一方、ロジスティック回帰は、「このデータがどのクラスに属するか」という結果そのものに直接注目する手法です。

データの分布の形を細かく仮定する代わりに、入力された特徴量 \mathbf{x} から、
クラスに属する確率 P(Y \mid \mathbf{x}) を直接推定するモデルを作ります。

このような、クラスを見分けるための確率を直接学習する考え方を、
「識別的なアプローチ」と呼びます。

このため、データが正規分布に従っているかどうかをあまり気にせずに使うことができ、
外れ値を含むデータや、分布が歪んでいるデータにも柔軟に対応できます。

また、各変数の係数を「オッズ比」として解釈できるため、
どの変数がどれくらい影響しているかを説明しやすい点も特徴です。

 

　使い分けの指針

LDAを選ぶべき場合としては、データがおおむね正規分布に従っていると考えられる場合、サンプルサイズが小さい場合、クラス内のばらつきや変数間の相関構造を明示的に考慮した分類を行いたい場合が挙げられます。

一方、ロジスティック回帰を選ぶべき場合としては、データが正規分布に従っていない可能性がある場合、外れ値が含まれている場合、また、各変数の影響をオッズ比として解釈したい場合が適しています。

実務では、両方の手法を試し、性能や解釈のしやすさを比較したうえで使い分けるのが一般的です。

なお、判別境界付近のデータでは、両モデルが出力する予測確率にわずかな違いが現れることがあります。これは、生成的モデルと識別的モデルというアプローチの違いが確率の解釈に反映されているためです。

 

まとめ

今回学んだことを振り返りましょう。

線形判別分析（LDA）は、各クラスのデータが多変量正規分布に従い、共分散行列が共通であると仮定します。ベイズの定理を使って事後確率を計算し、判別関数が最大となるクラスに分類します。

判別関数は \delta_k(\mathbf{x}) = \mathbf{x}^T \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_k - \frac{1}{2}\boldsymbol{\mu}_k^T \boldsymbol{\Sigma}^{-1} \boldsymbol{\mu}_k + \log(\pi_k) で表され、\mathbf{x} について線形なので、判別境界は直線になります。

LDAとロジスティック回帰は、どちらも線形の境界を引きますが、アプローチが異なります。LDAは分布を推定（生成的モデル）、ロジスティック回帰は確率を直接推定（識別的モデル）です。

使い分けとして、正規分布の仮定が妥当な場合やサンプルサイズが小さい場合はLDA、そうでない場合はロジスティック回帰が有利なことが多いです。

次回は「決定木」を学びます。

ロジスティック回帰やLDAは直線で境界を引きましたが、決定木は「もし身長が165cm以上なら…」「かつ体重が60kg以上なら…」のように、条件分岐を繰り返してデータを分類します。

人間の意思決定に近い、直感的に理解しやすい手法です。