データドリブンな意思決定がビジネスや政策、医療など多くの分野で重要視される現代において、因果効果の推定は欠かせない手法です。
因果効果を正確に推定することで、特定の施策が実際に期待される結果をもたらすかどうかを理解し、効率的な意思決定が可能になります。
因果推論は、ある変数(施策による処置または介入)が他の変数(結果)に与える影響を評価するプロセスです。これは、単なる相関関係とは異なり、一方が他方を引き起こす「原因と結果」の関係を探るものです。
回帰分析は、この因果推論を行う際の一般的な統計手法の一つで、目的変数と一つ以上の説明変数との関係をモデル化します。Pythonのデータサイエンスライブラリを利用して、これらの関係を簡単に調べることができます。
ここで「因果」という用語を用いていますが、回帰分析で因果は分かりませんし、他の手法でも恐らく厳密に因果を特定したり正確に推定することは不可能です。あくまでも「因果のようなもの」を特定したり、「因果のようなもの」の効果を推定するだけです。「因果のようなもの」なので単なる勘違いの可能性もあります。
Contents
回帰分析の基礎
回帰分析とは?
回帰分析は、目的変数 Y と一つまたは複数の説明変数 X 間の関係を数学的にモデル化する統計手法です。
線形回帰は最も基本的な回帰形式で、以下の線形方程式によりモデル化されます
\displaystyle Y=β_0 +β_1X_1+β_2X_2+\cdots+β_kX_k+ϵ- β_0,β_1,\cdots,β_k はモデルの係数(モデルパラメータ)であり、それぞれの説明変数が目的変数Yに与える影響の強さと方向を示します。
- ϵ は誤差項で、モデルが説明できない目的変数の変動を表します。
線形回帰モデルでは、係数β_0,β_1,\cdots,β_kを推定するために最小二乗法が一般的に用いられます。
この方法は、観測されたデータとモデルによる予測値の差(誤差)の二乗和が最小になるように係数を求めます。
具体的には、以下の式を最小化します。ここでY_iとX_{ji}は、それぞれi番目のデータ点の目的変数とj番目の説明変数の値です。
\displaystyle minimize\sum_{i=1}^n\left( Y_i−(β_0+β_1X_{1i}+\cdots+β_kX_{ki})\right)^2
回帰分析と相関関係
相関関係は、二つの量的変数間の線形関連の強さを示す指標です。
相関係数 r(通常、ピアソンの相関係数として知られる)は、次の式で計算されます。
\displaystyle r=\frac{\sum(X_i-\hat{X})\sum(Y_i-\hat{Y})}{\sqrt{\sum(X_i-\hat{X})^2(Y_i-\hat{Y})^2}}- X_i と Y_i はそれぞれの観測値
- \hat{X} と \hat{Y} はそれぞれの平均値
この係数は −1 から 1 の値を取り……
- 1 は完全な正の線形関連
- −1 は完全な負の線形関連
- 0 は無関連(無相関)
回帰分析における β_i の推定は、変数 _i と の間の線形関連を定量化しますが、これは相関係数 と密接に関連しています。
特に、単一の説明変数を持つ線形回帰モデルでは、係数 β_1 は X と Y の標準偏差の比率に相関係数を掛けたものに等しくなります。
\displaystyle \beta_1=r\frac{\sigma_Y}{\sigma_X}ここで、\sigma_X と \sigma_Y はそれぞれ X と Y の標準偏差です。
因果効果と相関の違い
相関関係は、二つの変数が統計的にどれくらい強く関連しているかを示す指標です。
相関係数は −1 から 1 の範囲で値を取り、正の値は正の関係を、負の値は負の関係を示します。相関係数が 0 に近い場合、変数間にはほとんどまたは全く関連がないことを意味します。
一方、因果関係は一つの変数(原因)が他の変数(結果)に影響を及ぼす関係です。
因果関係を確定するためには、単に統計的な関連を超えて、実験的な設定や厳密な統計的手法が必要です。特に、可能な交絡因子を制御することが重要です。
疑似相関(スプリアス相関)は、二つの変数が相関しているように見えるが、実際は第三の変数によって両者が影響を受けている状態を指します。
例えば、アイスクリームの売上と水泳事故が同時に増加する例は、夏という季節が共通の原因です。
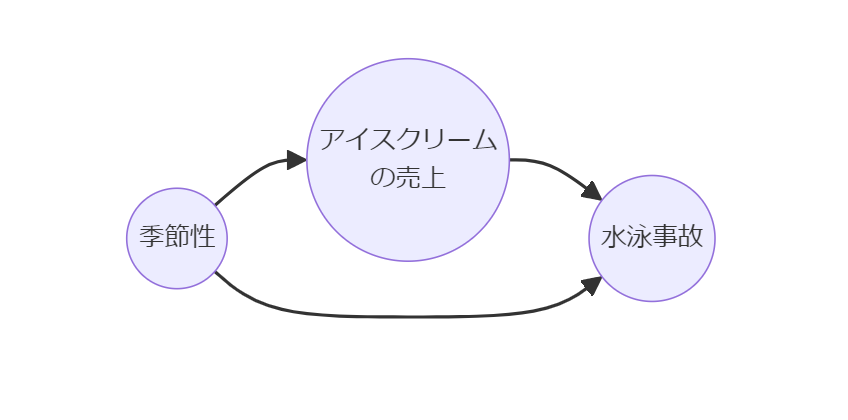
回帰分析において因果効果を推定する場合、適切なデータ収集、変数の選択、そして可能な交絡因子の制御が不可欠です。
交絡因子が適切にモデルに含まれていない場合、回帰分析によって得られる係数は偽の因果関係を示す可能性があります。
交絡因子の調整
交絡因子とは何か?
交絡因子は、説明変数と目的変数の両方に影響を与える変数で、これが含まれていない場合、誤った因果推論を引き起こす可能性があります。
交絡因子の存在により、本来の因果関係が歪められ、真の効果が過大または過小評価されることがあります。
たとえば、年齢は運動習慣と医療費の両方に影響を与える可能性があります。
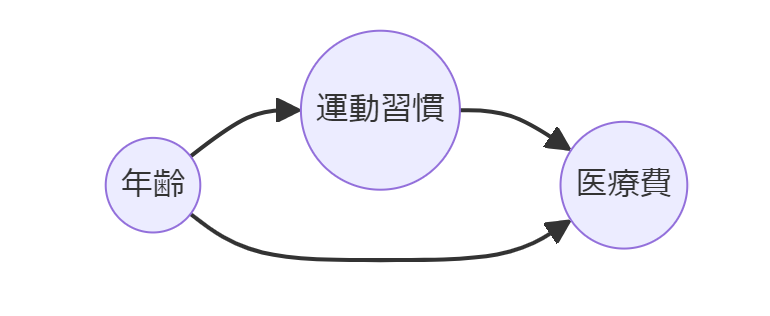
高齢者は若年者に比べて運動量が少なくなる傾向があり、同時に年齢が上がるにつれて医療費が増加する可能性が高くなります。
このような場合、年齢を考慮せずに運動習慣と医療費の関係だけを分析すると、運動習慣が医療費に与える真の効果を過小評価する可能性があります。
交絡因子の調整方法
交絡因子を適切に管理する方法には、主に次のようなものがあります。
回帰分析
回帰分析を用いると、一つ以上の交絡因子を説明変数としてモデルに含めることができます。これにより、他の説明変数に対する交絡因子の影響を数学的に「分離」し、独立変数の純粋な効果を推定できます。
層別分析
層別分析では、データを交絡因子(例: 年齢層、性別)に基づいて複数のサブグループに分け、各グループ内で分析を行います。これにより、交絡因子の各カテゴリ内での効果を個別に評価できます。
マッチング手法
マッチング手法、特に傾向スコアマッチングは、交絡因子を含む一連の変数から傾向スコア(処置を受ける確率)を算出し、このスコアが似ている対象同士をマッチングします。これにより、交絡因子の影響を均一化し、因果効果の推定精度を高めます。
逆確率重み付け(IPW)
IPWは、各個体が処置を受ける確率(傾向スコア)に基づいて重みを計算し、その重みを用いて分析を行います。これにより、サンプルの選択バイアスを補正し、より公平な比較が可能になります。
ダブルロバスト推定
ダブルロバスト推定は、傾向スコアモデリングとアウトカムモデリングの両方を利用する手法です。この方法は、どちらか一方のモデルが正しくなくても、もう一方が正確であれば正しい推定が可能です。
この中で最も手軽で簡単にできるのが、回帰分析を利用した方法です。
回帰分析を利用する理由と注意点
以下は、回帰分析が最も手軽で使い勝手がいい理由です。
馴染みがあり身近
回帰分析は、統計学において最も基本的かつ広く教育され知られている手法の一つです。また、主要なデータ分析ツールで広くサポートされているため、容易に利用できます。
技術的な複雑さが低い
回帰分析の数学的原理は直線的であり、計算プロセスも比較的シンプルです。回帰モデルでは、基本的な線形関係を用いるため、これらの複雑な手順が不要です。
実装の簡易性
データ分析系のプログラミング言語(R、Pythonなど)で実装する場合、回帰分析は数行のコードで済みます。技術的なハードルが低いため、初心者にも扱いやすく、迅速なデータ分析が可能です。
結果の解釈の容易さ
回帰分析の結果は直感的に理解しやすい形(係数としての効果量)で提供されます。これにより、説明変数が目的変数に与える影響の大きさと方向を簡単に解釈できます。
これらの理由により、多くの研究者や実務家にとって回帰分析は、交絡因子を調整する際の初めての選択肢となることが多いです。
このように回帰分析は非常に有用でアクセスしやすいツールですが、正確な結果を得るためにはいくつかの注意点を理解しておく必要があります。
以下は、回帰分析を行う際に考慮すべき主な注意点です。
線形性の仮定
回帰分析は、目的変数と説明変数間の線形関係を仮定しています。この仮定が適切でない場合(実際の関係が非線形である場合)、モデルはデータを正確に表現できず、誤った結果を導く可能性があります。非線形関係を持つデータには、多項式回帰や非線形回帰モデルを検討する必要があります。
独立性の仮定
回帰分析は、誤差項(残差)が互いに独立であるという仮定に基づいています。時間系列データや空間データなど、誤差項間に相関がある場合、標準的な回帰分析では適切な結果を得られないことがあります。このような場合、適切な手法(例えば、時系列分析や空間回帰分析)を用いる必要があります。
多重共線性
説明変数間に強い相関が存在する場合(多重共線性)、回帰係数の推定が不安定になり、解釈が困難になることがあります。この問題を解決するためには、相関の高い変数をモデルから除外するか、正則化技法(リッジ回帰、ラッソ回帰など)を使用することが一般的です。
外れ値の影響
外れ値は、回帰モデルに大きな影響を与える可能性があります。特に、外れ値が説明変数や目的変数のいずれかに存在する場合、回帰線の傾きや切片が大きく歪むことがあります。データを分析する前に外れ値を特定し、適切に対処することが重要です。
因果関係の誤解
相関関係が因果関係を意味するわけではないという原則は、回帰分析にも適用されます。回帰モデルで説明変数と目的変数の間に関連性が見つかったとしても、それが因果関係であると断定するには慎重な検討が必要です。特に、交絡因子が未調整の場合、誤った因果推論を引き起こすリスクがあります。
これらの注意点を理解し、適切に対応することで、回帰分析をより効果的に活用することができます。分析の計画段階でこれらの要素を検討することが、信頼性の高い結果を得るための鍵となります。
Pythonによる回帰調整の例
Pythonのscikit-learnライブラリを活用して、線形回帰モデルを構築し調整していきます。
データセット
サンプルデータとして、売上、広告費用、季節(春・夏・秋・冬)の3変数のデータセットを使います。
- sales:売上
- AdvertisingCost:広告費用 ※因果グラフ上はAdと表記
- Season:季節(春・夏・秋・冬)
- Spring:春、1Q(4月~6月)
- Summer:夏、2Q(7月~9月)
- Autumn:秋、3Q(10月~12月)
- Winter:冬、4Q(1月~3月)
季節(Season)が交絡因子です。
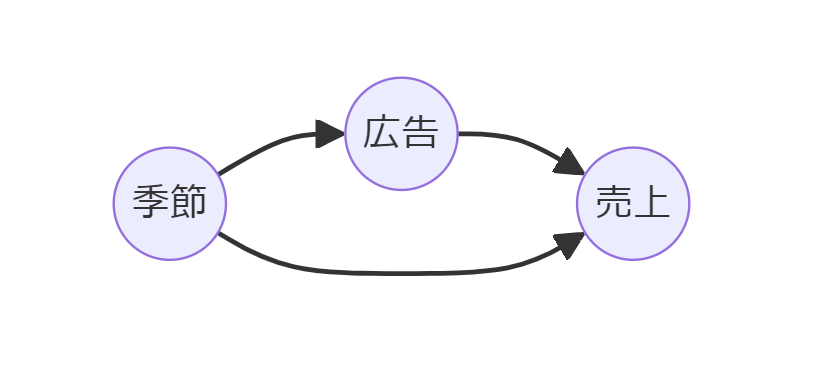
データセットは以下からダウンロードできます。
sample_data.csv
https://www.salesanalytics.co.jp/wc0m
準備
さっそく、必要なモジュールを読み込みます。
以下、コードです。
import pandas as pd import numpy as np from sklearn.preprocessing import OneHotEncoder from sklearn.linear_model import LinearRegression from sklearn.metrics import r2_score import matplotlib.pyplot as plt import networkx as nx
データセットを読み込みます。
以下、コードです。
#
# サンプルデータの読み込み
#
data = pd.read_csv(
'sample_data.csv',
index_col='YearQuarter'
)
print(data)
以下、実行結果です。
AdvertisingCost Season Sales YearQuarter 2018Q1 173.948705 Spring 200.987813 2018Q2 236.607780 Summer 257.144920 2018Q3 155.783976 Autumn 195.558620 2018Q4 138.961569 Winter 173.043713 2019Q1 185.076895 Spring 194.853063 ... ... ... ... 2066Q4 100.669615 Winter 154.127163 2067Q1 176.297145 Spring 203.448244 2067Q2 254.646060 Summer 275.155715 2067Q3 171.298147 Autumn 186.347508 2067Q4 131.890799 Winter 164.159509 [200 rows x 3 columns]
season(季節)変数がカテゴリカルデータのため、OneHotEncodeします。要は0-1変数に変換します。
以下、コードです。
#
# ワンホットエンコーデング(対象:Season)
#
encoder = OneHotEncoder(drop='first', sparse=False)
season_encoded = encoder.fit_transform(data[['Season']])
season_columns = encoder.get_feature_names_out(['Season'])
data_encoded = pd.concat([
data.drop(columns=['Season']),
pd.DataFrame(
season_encoded,
columns=season_columns,
index=data.index)],
axis=1)
print(data_encoded)
以下、実行結果です。たとえば、「Season_Spring」は春(1Q:4月~6月)に1、それ以外は0です。
AdvertisingCost Sales Season_Spring Season_Summer \
YearQuarter
2018Q1 173.948705 200.987813 1.0 0.0
2018Q2 236.607780 257.144920 0.0 1.0
2018Q3 155.783976 195.558620 0.0 0.0
2018Q4 138.961569 173.043713 0.0 0.0
2019Q1 185.076895 194.853063 1.0 0.0
... ... ... ... ...
2066Q4 100.669615 154.127163 0.0 0.0
2067Q1 176.297145 203.448244 1.0 0.0
2067Q2 254.646060 275.155715 0.0 1.0
2067Q3 171.298147 186.347508 0.0 0.0
2067Q4 131.890799 164.159509 0.0 0.0
Season_Winter
YearQuarter
2018Q1 0.0
2018Q2 0.0
2018Q3 0.0
2018Q4 1.0
2019Q1 0.0
... ...
2066Q4 1.0
2067Q1 0.0
2067Q2 0.0
2067Q3 0.0
2067Q4 1.0
[200 rows x 5 columns]
季節調整せず回帰モデル構築
まず、「季節変数(season)」を考慮せず、以下の線形回帰モデルを構築します。
- 目的変数:売上変数(Sales)
- 説明変数:マーケティング変数(AdvertisingCost)
以下、コードです。
'''
線形回帰モデルの構築
- 目的変数y:Sales
- 説明変数X:AdvertisingCost
'''
# 目的変数と説明変数
y = data_encoded['Sales']
X = data_encoded[['AdvertisingCost']]
# 線形回帰モデルの作成と訓練
model = LinearRegression()
model.fit(X, y)
# モデルパラメータの表示
print("モデルの係数: ", model.coef_)
print("モデルの切片: ", model.intercept_)
# 予測値の計算
predictions = model.predict(X)
# モデルの評価
print("R^2 Score: ", r2_score(y, predictions))
以下、実行結果です。
モデルの係数: [0.85526899] モデルの切片: 62.28235896289388 R^2 Score: 0.9298245760493467
R^2は決定係数で、モデルの説明力を表現し最大1(値は大きい方が良い)です。
マーケティング変数(AdvertisingCost)から売上変数(Sales)への係数は「0.85526899」です。
簡単に因果グラフを作ります。
以下、コードです。
# グラフのインスタンスを作成
G = nx.DiGraph()
# ノードを追加
G.add_nodes_from(['Ad', 'Season', 'Sales'])
# エッジを追加
G.add_edges_from([('Ad', 'Sales')])
# ノードとエッジの位置を指定
pos = {'Ad': (0, 1), 'Season': (1, 0), 'Sales': (2, 1)}
# グラフを描画
plt.figure(figsize=(10, 6))
nx.draw(
G,
pos,
with_labels=True,
node_size=5000,
node_color='skyblue',
font_size=18,
arrows=True,
arrowsize=30,
width=3,
)
# エッジラベルの追加
edge_labels = {('Ad', 'Sales'): '0.85526899'}
nx.draw_networkx_edge_labels(
G,
pos,
edge_labels=edge_labels,
font_size=20
)
plt.ylim(-0.1, 1.1)
plt.show()
以下、実行結果です。

季節調整して回帰モデル構築
次に、「季節変数(season)」を考慮し線形回帰モデルを構築します。
- 目的変数:売上変数(Sales)
- 説明変数:マーケティング変数(AdvertisingCost)、季節変数(season)
以下、コードです。
'''
線形回帰モデルの構築
- 目的変数y:Sales
- 説明変数X:AdvertisingCost, Season
'''
# 目的変数と説明変数
y = data_encoded['Sales']
X = data_encoded[['AdvertisingCost', 'Season_Summer', 'Season_Spring', 'Season_Winter']]
# 線形回帰モデルの作成と訓練
model = LinearRegression()
model.fit(X, y)
# モデルパラメータの表示
print("Model Coefficients: ", model.coef_)
print("Model Intercept: ", model.intercept_)
# 予測値の計算
predictions = model.predict(X)
# モデルの評価
print("R^2 Score: ", r2_score(y, predictions))
以下、実行結果です。
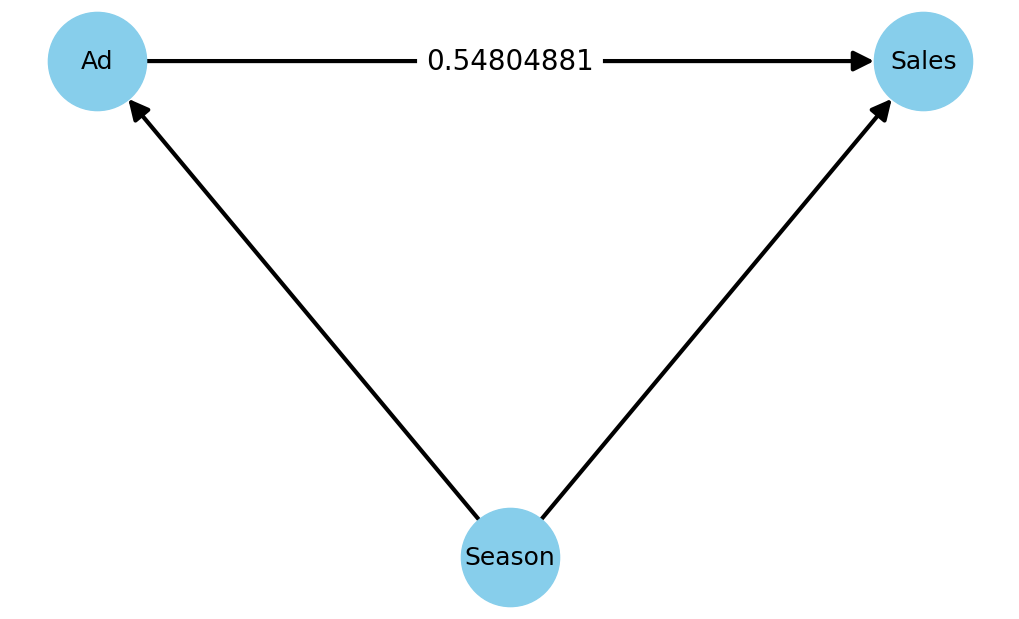
Model Coefficients: [ 0.54804881 33.15003318 7.68011252 -7.85504313] Model Intercept: 103.01837730341886 R^2 Score: 0.9417953198720368
マーケティング変数(AdvertisingCost)から売上変数(Sales)への係数が、「0.85526899」から「0.54804881」へ変化していることが分かります。
簡単に因果グラフを作ります。
以下、コードです。
# グラフのインスタンスを作成
G = nx.DiGraph()
# ノードを追加
G.add_nodes_from(['Ad', 'Season', 'Sales'])
# エッジを追加
G.add_edges_from([('Ad', 'Sales'), ('Season', 'Sales'), ('Season', 'Ad')])
# ノードとエッジの位置を指定
pos = {'Ad': (0, 1), 'Season': (1, 0.5), 'Sales': (2, 1)}
# グラフを描画
plt.figure(figsize=(10, 6))
nx.draw(
G,
pos,
with_labels=True,
node_size=5000,
node_color='skyblue',
font_size=18,
arrows=True,
arrowsize=30,
width=3
)
# エッジラベルの追加
edge_labels = {('Ad', 'Sales'): '0.54804881'}
nx.draw_networkx_edge_labels(
G,
pos,
edge_labels=edge_labels,
font_size=20
)
plt.show()
以下、実行結果です。
交絡因子調整をステップByステップで実施
回帰調整をもう少し丁寧に説明します。
季節が交絡因子です。

この交絡因子を、「マーケティング変数(AdvertisingCost)」と「売上変数(Sales)」から除去する必要があります。この除去を調整と呼んでいます。
除去の方法は簡単です。線形回帰モデルを構築するだけです。
マーケティング変数(AdvertisingCost)から季節の影響を除去
まず、「マーケティング変数(AdvertisingCost)」から季節の影響を除去します。
具体的に、以下の線形回帰モデルを構築します。
- 目的変数:マーケティング変数(AdvertisingCost)
- 説明変数:季節変数(season)
このとき重要なのは、構築した線形回帰モデルの残差です。
この残差は、「マーケティング変数(AdvertisingCost)」から「季節変数(season)」の影響を除去した値だからです。
では、実際に求めてみます。
以下、コードです。
'''
線形回帰モデルの構築
- 目的変数y:AdvertisingCost
- 説明変数X:Season
'''
# 目的変数と説明変数
y = data_encoded['AdvertisingCost']
X = data_encoded[['Season_Summer', 'Season_Spring', 'Season_Winter']]
# 線形回帰モデルの作成と訓練
model = LinearRegression()
model.fit(X, y)
# モデルパラメータの表示
print("モデルの係数: ", model.coef_)
print("モデルの切片: ", model.intercept_)
# 予測値の計算
predictions = model.predict(X)
# 予測値の計算
ad_residuals = y - predictions
# モデルの評価
print("R^2 Score: ", r2_score(y, predictions))
以下、実行結果です。
モデルの係数: [101.11857272 28.82800764 -18.81328408] モデルの切片: 131.6456360255056 R^2 Score: 0.9114733052856144
R^2がそこそこ高く、「季節変数(season)」に説明力があることが分かります。
また残差もしっかり「ad_residuals」に格納しました。
この残差が、「マーケティング変数(AdvertisingCost)」から「季節変数(season)」の影響を除去した値です。
売上変数(Sales)から季節の影響を除去
次に、「売上変数(Sales)」から季節の影響を除去します。
具体的に、以下の線形回帰モデルを構築します。
- 目的変数:売上変数(Sales)
- 説明変数:季節変数(season)
このとき重要なのは、構築した線形回帰モデルの残差です。
この残差は、「売上変数(Sales)」から「季節変数(season)」の影響を除去した値だからです。
では、実際に求めてみます。
以下、コードです。
'''
線形回帰モデルの構築
- 目的変数y:Sales
- 説明変数X:Season
'''
# 目的変数と説明変数
y = data_encoded['Sales']
X = data_encoded[['Season_Summer', 'Season_Spring', 'Season_Winter']]
# 線形回帰モデルの作成と訓練
model = LinearRegression()
model.fit(X, y)
# モデルパラメータの表示
print("Model Coefficients: ", model.coef_)
print("Model Intercept: ", model.intercept_)
# 予測値の計算
predictions = model.predict(X)
# 予測値の計算
Sales_residuals = y - predictions
# モデルの評価
print("R^2 Score: ", r2_score(y, predictions))
以下、実行結果です。
Model Coefficients: [ 88.56794616 23.47926767 -18.16564099] Model Intercept: 175.1666108609082 R^2 Score: 0.9079959741799482
R^2がそこそこ高く、「季節変数(season)」に説明力があることが分かります。
また残差もしっかり「y_residuals」に格納しました。
この残差が、「売上変数(Sales)」から「季節変数(season)」の影響を除去した値です。
残差同士で線形回帰
最後に、ここまでに求めた以下の「残差」(季節調整したデータ)を使い線形回帰モデルを構築します。
- 目的変数:売上変数の残差(Sales_residuals)
- 説明変数:マーケティング変数の残差(ad_residuals)
以下、コードです。
'''
線形回帰モデルの構築
- 目的変数y:Sales(res)
- 説明変数X:Ad(res)
'''
# 目的変数と説明変数
y = Sales_residuals
X = ad_residuals.to_frame()
# 線形回帰モデルの作成と訓練
model = LinearRegression()
model.fit(X, y)
# モデルパラメータの表示
print("モデルの係数: ", model.coef_)
print("モデルの切片: ", model.intercept_)
# 予測値の計算
predictions = model.predict(X)
# モデルの評価
print("R^2 Score: ", r2_score(y, predictions))
以下、実行結果です。
モデルの係数: [0.54804881] モデルの切片: -5.576789628096072e-15 R^2 Score: 0.3673681166756315
マーケティング変数(AdvertisingCost)から売上変数(Sales)への係数は「0.54804881」です。
簡単に因果グラフを作ります。
以下、コードです。
# グラフのインスタンスを作成
G = nx.DiGraph()
# ノードを追加
G.add_nodes_from(['Ad\n(res)', 'Sales\n(res)'])
# エッジを追加
G.add_edges_from([('Ad\n(res)', 'Sales\n(res)')])
# ノードとエッジの位置を指定
pos = {'Ad\n(res)': (0, 1), 'Sales\n(res)': (2, 1)}
# グラフを描画
plt.figure(figsize=(10, 6))
nx.draw(
G,
pos,
with_labels=True,
node_size=5000,
node_color='skyblue',
font_size=18,
arrows=True,
arrowsize=30,
width=3
)
# エッジラベルの追加
edge_labels = {('Ad\n(res)', 'Sales\n(res)'): '0.54804881'}
nx.draw_networkx_edge_labels(
G,
pos,
edge_labels=edge_labels,
font_size=20
)
plt.show()
以下、実行結果です。

- Sales(res):売上変数の残差(Sales_residuals)
- Ad(res):マーケティング変数の残差(ad_residuals)
以下の線形回帰モデルと、同じ結果になったかと思います。
- 目的変数:売上変数(Sales)
- 説明変数:マーケティング変数(AdvertisingCost)、季節変数(season)

要は、交絡因子を線形回帰モデルに説明変数として組み込むことで、交絡因子を調整した結果を得ることができます。
まとめ
因果効果の推定は、ビジネスや政策の意思決定において重要な役割を果たします。
データから単なる相関関係ではなく因果関係を特定するための手法が必要であり、その中でも回帰分析は、説明変数の効果を適切に推定するための主要な手法の一つです。
回帰分析によって交絡因子を含めた上で目的変数との関係性をモデル化することで、説明変数の効果を明確にできます。
因果効果の推定は、データサイエンスの重要なトピックであり、機械学習技術の進歩に伴い、新たなアプローチが求められています。
例えば、因果グラフや深層学習を活用した因果推論は、複雑な問題への新たな解決策となるでしょう。
ビジネス戦略や政策立案に広く応用されるため、データサイエンティストにとって因果推論の知識は今後も重要となります。

