時系列データの予測は、企業が将来の売上や需要を予測し、意思決定に活用するための重要なツールです。近年、機械学習技術の発展により、時系列予測はより高精度かつ柔軟なアプローチが求められています。
Pythonライブラリ「mlforecast」を活用することで、テーブルデータ系の機械学習モデルで時系列予測を実施することができます。
mlforecastはシンプルなAPIを提供しながら、複数のアルゴリズムやハイパーパラメータ調整を容易に行える点が魅力です。
前回の記事「Python mlforecast で始める機械学習時系列予測入門」では、mlforecastの基本的な導入方法と基本的なモデル構築についてお話ししました。
Python mlforecast で始める 機械学習 時系列予測 入門– 第1回:Python 時系列予測ライブラリ mlforecast の導入 –
今回は、さらに一歩進んで、AirPassengersDFデータを使い、単一および複数の機械学習モデルを用いた時系列予測の構築を行います。
また、ハイパーパラメータの調整に関しても、Scikit-learnのGridSearchCVとOptunaを用いた自動調整の実践的なアプローチを紹介します。
Contents
mlforecastのインストール
Pythonのパッケージ管理システムであるpipを使って簡単にインストールできます。
以下、コードです。
pip install mlforecast
condaでのインストールは以下です。
conda install -c conda-forge mlforecast
AirPassengersDFを用いたデータ準備
使用するデータセットは、「AirPassengersDF」です。このデータセットは、国際航空旅客の月次データで、1949年から1960年までの乗客数を示しています。
これは、時系列予測において非常に有名なデータセットであり、季節性とトレンドを持つため、時系列分析の実践的な例として最適です。
まず、データを読み込み、データ構造を確認します。
以下、コードです。
import pandas as pd
# データの読み込み
Y_df = pd.read_csv(
'https://datasets-nixtla.s3.amazonaws.com/air-passengers.csv',
parse_dates=['ds']
)
# データの可視化
Y_df.plot(y='y', x='ds')
plt.show()
# データ確認
print(Y_df)
以下、実行結果です。
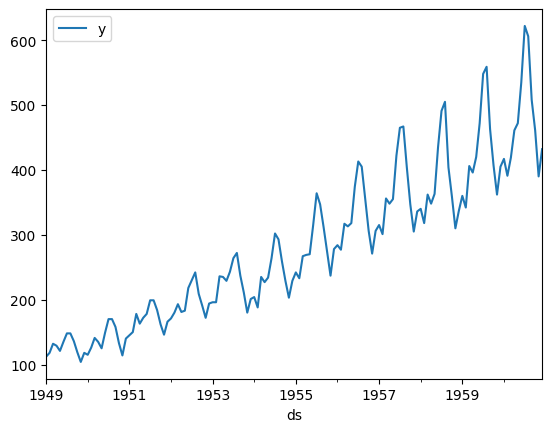
unique_id ds y 0 AirPassengers 1949-01-01 112 1 AirPassengers 1949-02-01 118 2 AirPassengers 1949-03-01 132 3 AirPassengers 1949-04-01 129 4 AirPassengers 1949-05-01 121 .. ... ... ... 139 AirPassengers 1960-08-01 606 140 AirPassengers 1960-09-01 508 141 AirPassengers 1960-10-01 461 142 AirPassengers 1960-11-01 390 143 AirPassengers 1960-12-01 432 [144 rows x 3 columns]
データ構造
- unique_id: 時系列を識別するID(本例では単一の時系列のため1つ)
- ds: 観測日付
- y: 月ごとの乗客数
基本的な時系列予測モデルの構築
ここでは、mlforecastを用いてAirPassengersDFデータに対する基本的な時系列予測モデルを構築します。
今回は単一モデルとしてランダムフォレスト回帰モデルを使用し、過去の値を特徴量として学習させます。
モデル構築の準備
mlforecastを使用するため、まずライブラリをインポートし、モデル構築の準備を行います。
先ず、学習データ期間とテストてデータ期間に分けます。直近12カ月間がテストデータ期間です。
以下、コードです。
# データの分割
Y_train_df = Y_df[Y_df.ds <= '1959-12-31'] # 1959年までを学習データ
Y_test_df = Y_df[Y_df.ds > '1959-12-31'] # 1960年以降をテストデータ
# データ確認
print(
'学習データ(1959年まで)\n',Y_train_df,'\n\n',
'テストデータ(1960年以降)\n',Y_test_df)
以下、実行結果です。
学習データ(1959年まで)
unique_id ds y
0 AirPassengers 1949-01-01 112
1 AirPassengers 1949-02-01 118
2 AirPassengers 1949-03-01 132
3 AirPassengers 1949-04-01 129
4 AirPassengers 1949-05-01 121
.. ... ... ...
127 AirPassengers 1959-08-01 559
128 AirPassengers 1959-09-01 463
129 AirPassengers 1959-10-01 407
130 AirPassengers 1959-11-01 362
131 AirPassengers 1959-12-01 405
[132 rows x 3 columns]
テストデータ(1960年以降)
unique_id ds y
132 AirPassengers 1960-01-01 417
133 AirPassengers 1960-02-01 391
134 AirPassengers 1960-03-01 419
135 AirPassengers 1960-04-01 461
136 AirPassengers 1960-05-01 472
137 AirPassengers 1960-06-01 535
138 AirPassengers 1960-07-01 622
139 AirPassengers 1960-08-01 606
140 AirPassengers 1960-09-01 508
141 AirPassengers 1960-10-01 461
142 AirPassengers 1960-11-01 390
143 AirPassengers 1960-12-01 432
時系列特徴量を追加していきます。時系列特徴量については、以下を参考にしてください。
時系列特徴量の中には、mlforecastのモデルのインスタンスの中に組み込むもの(ラグ特徴量やローリング特徴量など)と、そうでないもの(周期を表現する三角関数特徴量など)があります。
周期を表現する三角関数特徴量を追加します。mlforecastにはそのための機能があります。
以下、コードです。
from utilsforecast.feature_engineering import fourier
transformed_df, future_df = fourier(
Y_df, # データ
freq='M', # 月単位
season_length=12, # 季節周期
k=2, # フーリエ項の数(sinとcosのセット数)
h=12, # 予測期間
)
# データ確認
print(
'学習データ(1959年まで)\n',transformed_df,'\n\n',
'テストデータ(1960年以降)\n',future_df)
以下、実行結果です。
学習データ(1959年まで)
unique_id ds y sin1_12 sin2_12 cos1_12 \
0 AirPassengers 1949-01-01 112 5.000000e-01 8.660254e-01 8.660254e-01
1 AirPassengers 1949-02-01 118 8.660254e-01 8.660254e-01 5.000000e-01
2 AirPassengers 1949-03-01 132 1.000000e+00 -8.742278e-08 -4.371139e-08
3 AirPassengers 1949-04-01 129 8.660254e-01 -8.660254e-01 -5.000001e-01
4 AirPassengers 1949-05-01 121 5.000001e-01 -8.660254e-01 -8.660254e-01
.. ... ... ... ... ... ...
139 AirPassengers 1960-08-01 606 -8.660276e-01 8.660210e-01 -4.999962e-01
140 AirPassengers 1960-09-01 508 -1.000000e+00 -6.731475e-06 3.365737e-06
141 AirPassengers 1960-10-01 461 -8.660243e-01 -8.660277e-01 5.000020e-01
142 AirPassengers 1960-11-01 390 -4.999989e-01 -8.660241e-01 8.660260e-01
143 AirPassengers 1960-12-01 432 1.907981e-07 3.815962e-07 1.000000e+00
cos2_12
0 0.500000
1 -0.500000
2 -1.000000
3 -0.500000
4 0.500000
.. ...
139 -0.500008
140 -1.000000
141 -0.499996
142 0.500002
143 1.000000
[144 rows x 7 columns]
テストデータ(1960年以降)
unique_id ds sin1_12 sin2_12 cos1_12 cos2_12
0 AirPassengers 1960-12-31 0.499999 0.866025 0.866026 0.500001
1 AirPassengers 1961-01-31 0.866028 0.866020 0.499995 -0.500010
2 AirPassengers 1961-02-28 1.000000 -0.000009 -0.000005 -1.000000
3 AirPassengers 1961-03-31 0.866024 -0.866029 -0.500003 -0.499994
4 AirPassengers 1961-04-30 0.499998 -0.866023 -0.866027 0.500004
5 AirPassengers 1961-05-31 -0.000001 0.000003 -1.000000 1.000000
6 AirPassengers 1961-06-30 -0.500000 0.866026 -0.866025 0.499999
7 AirPassengers 1961-07-31 -0.866025 0.866026 -0.500001 -0.499999
8 AirPassengers 1961-08-31 -1.000000 -0.000012 0.000006 -1.000000
9 AirPassengers 1961-09-30 -0.866023 -0.866030 0.500004 -0.499992
10 AirPassengers 1961-10-31 -0.499997 -0.866022 0.866027 0.500007
11 AirPassengers 1961-11-30 0.000003 0.000005 1.000000 1.000000
もし、外生変数(説明変数)などがある場合には、この段階で追加しておきます。この三角関数特徴量は外生変数として追加されているということです。
以後、学習データとしてtransformed_dfを使い、テストデータを予測するときにはfuture_dfを使います。
モデルの学習
モデルのインスタンスを作り学習します。
インスタンスの中に、ラグ特徴量などを含めた場合にはラグ特徴量を生成したり、その影響で欠損値などが発生したりします。そのための前処理を実施しなければなりません。
以下、コードです。インスタンス生成後に前処理を実施しています。
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from mlforecast.lag_transforms import ExpandingMean, RollingMean
from sklearn.ensemble import RandomForestRegressor
# モデルの設定
model = RandomForestRegressor(
n_estimators=100,
random_state=42
)
# MLForecastのインスタンスを作成
fcst = MLForecast(
models=model,
freq='M', # 月単位
lags=[1], # ラグ特徴量(過去1期)
lag_transforms={
1: [RollingMean(window_size=12)], #ローリング特徴量(前期までの過去12期移動平均)
1: [ExpandingMean()], #エクスパンディング特徴量(前期までの全期間平均)
},
target_transforms=[Differences([1])], # 差分処理(過去1期からの差分)
)
# データの前処理
preprocessed_df = fcst.preprocess(
transformed_df, # 学習データ
static_features=[], # 静的特徴量(今回はなし)
dropna=True, # 欠損値の削除
)
print(preprocessed_df)
以下、実行結果です。
unique_id ds y sin1_12 sin2_12 cos1_12 \
2 AirPassengers 1949-03-01 14.0 1.000000e+00 -8.742278e-08 -4.371139e-08
3 AirPassengers 1949-04-01 -3.0 8.660254e-01 -8.660254e-01 -5.000001e-01
4 AirPassengers 1949-05-01 -8.0 5.000001e-01 -8.660254e-01 -8.660254e-01
5 AirPassengers 1949-06-01 14.0 -8.742278e-08 1.748456e-07 -1.000000e+00
6 AirPassengers 1949-07-01 13.0 -5.000002e-01 8.660256e-01 -8.660253e-01
.. ... ... ... ... ... ...
139 AirPassengers 1960-08-01 -16.0 -8.660276e-01 8.660210e-01 -4.999962e-01
140 AirPassengers 1960-09-01 -98.0 -1.000000e+00 -6.731475e-06 3.365737e-06
141 AirPassengers 1960-10-01 -47.0 -8.660243e-01 -8.660277e-01 5.000020e-01
142 AirPassengers 1960-11-01 -71.0 -4.999989e-01 -8.660241e-01 8.660260e-01
143 AirPassengers 1960-12-01 42.0 1.907981e-07 3.815962e-07 1.000000e+00
cos2_12 lag1 expanding_mean_lag1
2 -1.000000 6.0 6.000000
3 -0.500000 14.0 10.000000
4 0.500000 -3.0 5.666667
5 1.000000 -8.0 2.250000
6 0.500000 14.0 4.600000
.. ... ... ...
139 -0.500008 87.0 3.695652
140 -1.000000 -16.0 3.553957
141 -0.499996 -98.0 2.828571
142 0.500002 -47.0 2.475177
143 1.000000 -71.0 1.957747
[142 rows x 9 columns]
このデータを使い学習します。
ちなみに、今回は表示用にpreprocessed_dfに値を代入していますが、学習時にはこの前処理を反映した学習を実施しますので、fitメソッドの引数にtransformed_dfをそのまま指定します。
以下、コードです。
# 学習
fcst.fit(
transformed_df,
static_features=[]
)
予測と精度検証
モデルを学習させた後、テストデータに対して予測を行います。
# 予測を行う(12か月先までの予測)
forecast = fcst.predict(
12, # 予測期間
X_df=future_df, # 予測期間の外生変数(今回は三角関数特徴量)
)
# 結果の表示
print(forecast)
以下、実行結果です。
unique_id ds RandomForestRegressor 0 AirPassengers 1960-12-31 436.980011 1 AirPassengers 1961-01-31 416.190002 2 AirPassengers 1961-02-28 446.230011 3 AirPassengers 1961-03-31 459.020020 4 AirPassengers 1961-04-30 463.250031 5 AirPassengers 1961-05-31 515.860046 6 AirPassengers 1961-06-30 563.290039 7 AirPassengers 1961-07-31 553.620056 8 AirPassengers 1961-08-31 514.540039 9 AirPassengers 1961-09-30 476.270050 10 AirPassengers 1961-10-31 454.630066 11 AirPassengers 1961-11-30 485.720062
精度評価します。
以下、コードです。
from sklearn.metrics import (
mean_absolute_error, # MAE
mean_absolute_percentage_error, # MAPE
mean_squared_error, # MSE
r2_score, # R2
)
# 予測 'y' 列を使って評価指標を計算(文字列列を無視するため)
forecast_values = forecast['RandomForestRegressor'].values
actual_values = Y_test_df['y'].values
# 精度評価指標の計算
mae = mean_absolute_error(actual_values, forecast_values)
mape = mean_absolute_percentage_error(actual_values, forecast_values)
mse = mean_squared_error(actual_values, forecast_values)
rmse = mean_squared_error(actual_values, forecast_values, squared=False)
r2 = r2_score(actual_values, forecast_values)
# 精度評価指標の表示
print(
'MAE:',mae,
'\nMAPE:',mape,
'\nMSE:',mse,
'\nRMSE:',rmse,
'\nR2:',r2,
)
以下、実行結果です。
MAE: 29.460004170735676 MAPE: 0.06273562629706837 MSE: 1312.615479398286 RMSE: 36.230035597529934 R2: 0.7630432238413292
以下に各精度指標の説明とその見方を示します。
MAE (Mean Absolute Error)
- 平均絶対誤差は、予測値と実際の値の差の絶対値の平均を示します。
- 値が小さいほど、予測が実際の値に近いことを示します。
- 今回のMAEは13.21であり、これは予測が平均して約29.46の誤差を持っていることを意味します。
MAPE (Mean Absolute Percentage Error)
- 平均絶対パーセント誤差は、予測誤差を実際の値で割ったものの平均を示します。
- 値が小さいほど、予測が実際の値に近いことを示します。
- 今回のMAPEは0.0627であり、これは予測が平均して約6.27%の誤差を持っていることを意味します。
MSE (Mean Squared Error)
- 平均二乗誤差は、予測値と実際の値の差の二乗の平均を示します。
- 値が小さいほど、予測が実際の値に近いことを示します。
- 今回のMSEは1312.62であり、これは予測が平均して約1312.62の二乗誤差を持っていることを意味します。
RMSE (Root Mean Squared Error)
- 二乗平均平方根誤差は、MSEの平方根を取ったもので、元のデータの単位で誤差を示します。
- 値が小さいほど、予測が実際の値に近いことを示します。
- 今回のRMSEは36.23であり、これは予測が平均して約36.23の誤差を持っていることを意味します。
R2 (R-squared)
- 決定係数は、モデルがデータの分散をどれだけ説明できるかを示します。
- 値は0から1の間で、1に近いほどモデルの予測精度が高いことを示します。
- 今回のR2は0.763であり、これはモデルがデータの約76.3%の分散を説明できていることを意味します。
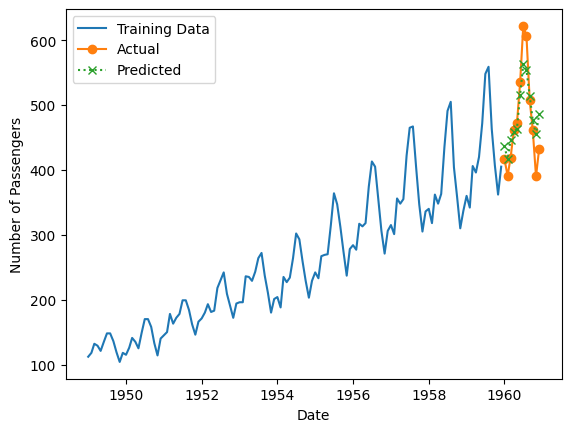
最後に、学習データ期間も含めグラフでプロットします。
以下、コードです。
# 学習データ期間のデータ
y_train = Y_train_df.set_index('ds')['y']
# グラフ表示
plt.plot(y_train, label='Training Data')
plt.plot(Y_test_df['ds'], actual_values, label='Actual', marker='o')
plt.plot(Y_test_df['ds'], forecast_values, label='Predicted', marker='x', linestyle=':')
plt.xlabel('Date')
plt.ylabel('Number of Passengers')
plt.legend()
plt.show()
以下、実行結果です。
ハイパーパラメータの調整
モデルの精度を向上させるためには、ハイパーパラメータの調整が重要です。
Scikit-learnのGridSearchCVを用いることで、複数のハイパーパラメータの組み合わせをグリッドサーチ(全通り探索)で探索し、最適なパラメータを見つけることができます。
大きな違いは、MLForecastの設定でmodelsにGridSearchCVのインスタンスを設定することです。
まず、GridSearchCVのインスタンスを生成します。クラスバリデーションは、時系列のクラスバリデーションを指定しています。
以下、コードです。
from sklearn.model_selection import TimeSeriesSplit, GridSearchCV
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from mlforecast.lag_transforms import ExpandingMean, RollingMean
from sklearn.ensemble import RandomForestRegressor
# モデルの設定
model = RandomForestRegressor(
n_estimators=100,
random_state=42,
)
# ハイパーパラメータ候補を修正
param_grid = {
'n_estimators': [10, 50, 100, 200],
'max_depth': [2, 10, 20, None]
}
# TimeSeriesSplitによる時系列CV
time_series_cv = TimeSeriesSplit(n_splits=5)
# GridSearchCVのインスタンス作成
grid_search = GridSearchCV(
estimator=RandomForestRegressor(random_state=42),
param_grid=param_grid,
cv=time_series_cv,
scoring='neg_mean_absolute_error'
)
このGridSearchCVのインスタンスを、MLForecastのmodelsに設定します。
以下、コードです。
# MLForecastのインスタンスを作成
fcst = MLForecast(
models=grid_search,
freq='M', # 月単位
lags=[1], # ラグ特徴量(過去1期)
lag_transforms={
1: [RollingMean(window_size=12)], #ローリング特徴量(前期までの過去12期移動平均)
1: [ExpandingMean()], #エクスパンディング特徴量(前期までの全期間平均)
},
target_transforms=[Differences([1])], # 差分処理(過去1期からの差分)
)
あとは、先ほどとほぼ同じコードで実施するため、まとめて記載します。前処理⇒学習⇒予測⇒精度評価と進みます。
以下、コードです。
# データの前処理
fcst.preprocess(
transformed_df, # 学習データ
static_features=[], # 静的特徴量(今回はなし)
dropna=True, # 欠損値の削除
)
# 学習
fcst.fit(
transformed_df,
static_features=[]
)
# 予測を行う(12か月先までの予測)
forecast = fcst.predict(
12, # 予測期間
X_df=future_df, # 予測期間の外生変数(今回は三角関数特徴量)
)
# 結果の表示
print(forecast)
from sklearn.metrics import (
mean_absolute_error, # MAE
mean_absolute_percentage_error, # MAPE
mean_squared_error, # MSE
r2_score, # R2
)
# 予測 'y' 列を使って評価指標を計算(文字列列を無視するため)
forecast_values = forecast['GridSearchCV'].values
actual_values = Y_test_df['y'].values
# 精度評価指標の計算
mae = mean_absolute_error(actual_values, forecast_values)
mape = mean_absolute_percentage_error(actual_values, forecast_values)
mse = mean_squared_error(actual_values, forecast_values)
rmse = mean_squared_error(actual_values, forecast_values, squared=False)
r2 = r2_score(actual_values, forecast_values)
# 精度評価指標の表示
print(
'MAE:',mae,
'\nMAPE:',mape,
'\nMSE:',mse,
'\nRMSE:',rmse,
'\nR2:',r2,
)
import matplotlib.pyplot as plt
# 学習データ期間のデータ
y_train = Y_train_df.set_index('ds')['y']
# グラフ表示
plt.plot(y_train, label='Training Data')
plt.plot(Y_test_df['ds'], actual_values, label='Actual', marker='o')
plt.plot(Y_test_df['ds'], forecast_values, label='Predicted', marker='x', linestyle=':')
plt.xlabel('Date')
plt.ylabel('Number of Passengers')
plt.legend()
plt.show()
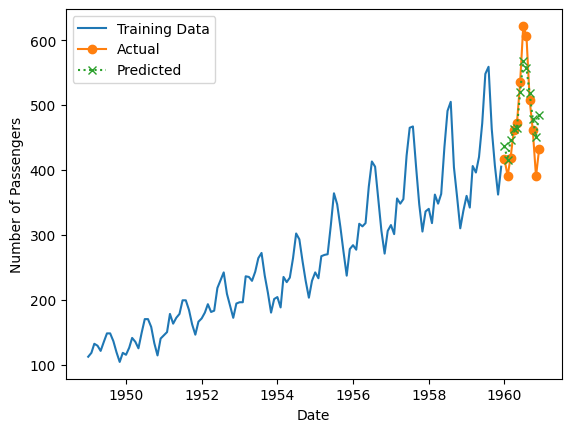
以下、実行結果です。
unique_id ds GridSearchCV 0 AirPassengers 1960-12-31 436.440002 1 AirPassengers 1961-01-31 415.399994 2 AirPassengers 1961-02-28 446.539978 3 AirPassengers 1961-03-31 462.819977 4 AirPassengers 1961-04-30 465.199982 5 AirPassengers 1961-05-31 520.000000 6 AirPassengers 1961-06-30 567.820007 7 AirPassengers 1961-07-31 556.660034 8 AirPassengers 1961-08-31 517.880005 9 AirPassengers 1961-09-30 478.739990 10 AirPassengers 1961-10-31 451.359985 11 AirPassengers 1961-11-30 485.059998 MAE: 28.37999216715495 MAPE: 0.06064630546069558 MSE: 1197.409423181399 RMSE: 34.60360419351428 R2: 0.7838405221389404
複数モデルを用いた予測の比較と活用
単一のモデルを使用するだけでなく、複数のモデルを用いることで、予測の精度をさらに向上させることができます。
複数モデルによる予測後に、アンサンブルしてもいいでしょう。今回は、各モデルの予測結果を出力するところまでを実施します。
2つのパターンのコード例を示します。
- ハイパーパラメータ調整しない
- ハイパーパラメータ調整をする
ハイパーパラメータ調整しない
MLForecastの設定でmodelsに複数のモデルのインスタンスを設定するだけです。リストもしくは辞書として渡します。
以下、コードです。
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from mlforecast.lag_transforms import ExpandingMean, RollingMean
from sklearn.ensemble import RandomForestRegressor
from lightgbm import LGBMRegressor
from xgboost import XGBRegressor
# モデルのリスト
models = [
RandomForestRegressor(n_estimators=100, random_state=42),
LGBMRegressor(n_estimators=100, random_state=42),
XGBRegressor(n_estimators=100, random_state=42),
]
# MLForecastのインスタンスを作成
fcst = MLForecast(
models=models,
freq='M', # 月単位
lags=[1], # ラグ特徴量(過去1期)
lag_transforms={
1: [RollingMean(window_size=12)], #ローリング特徴量(前期までの過去12期移動平均)
1: [ExpandingMean()], #エクスパンディング特徴量(前期までの全期間平均)
},
target_transforms=[Differences([1])], # 差分処理(過去1期からの差分)
)
このコードの場合は、モデルのリストを作成し、MLForecastのmodelsに設定しているだけです。
あとは、先ほどとほぼ同じコードで実施するため、まとめて記載します。前処理⇒学習⇒予測⇒精度評価と進みます。
以下、コードです。
# データの前処理
fcst.preprocess(
transformed_df, # 学習データ
static_features=[], # 静的特徴量(今回はなし)
dropna=True, # 欠損値の削除
)
# 学習
fcst.fit(
transformed_df,
static_features=[]
)
# 予測を行う(12か月先までの予測)
forecast = fcst.predict(
12, # 予測期間
X_df=future_df, # 予測期間の外生変数(今回は三角関数特徴量)
)
# 結果の表示
print(forecast)
from sklearn.metrics import (
mean_absolute_error, # MAE
mean_absolute_percentage_error, # MAPE
mean_squared_error, # MSE
r2_score, # R2
)
# 予測 'y' 列を使って評価指標を計算(文字列列を無視するため)
y_true = Y_test_df['y'].values
# 使用するモデルの名称リスト
model_names = ['RandomForestRegressor', 'LGBMRegressor', 'XGBRegressor']
# 各モデルに対して評価指標を計算
for model_name in model_names:
# 予測結果を取得
y_pred = forecast[model_name].values
# 各指標を計算
mae = mean_absolute_error(y_true, y_pred) # MAEの計算
mape = mean_absolute_percentage_error(y_true, y_pred) # MAPEの計算
mse = mean_squared_error(y_true, y_pred) # MSEの計算
rmse = mean_squared_error(y_true, y_pred, squared=False) # RMSEの計算
r2 = r2_score(y_true, y_pred) # R2の計算
# 計算結果を表示
print(f"Model: {model_name}")
print('MAE:', mae)
print('MAPE:', mape)
print('MSE:', mse)
print('RMSE:', rmse)
print('R2:', r2)
print('\n' + '-'*30 + '\n')
以下、実行結果です。
unique_id ds RandomForestRegressor LGBMRegressor \
0 AirPassengers 1960-12-31 436.980011 434.960876
1 AirPassengers 1961-01-31 416.190002 424.461670
2 AirPassengers 1961-02-28 446.230011 445.131042
3 AirPassengers 1961-03-31 459.020020 443.943268
4 AirPassengers 1961-04-30 463.250031 446.868042
5 AirPassengers 1961-05-31 515.860046 489.621429
6 AirPassengers 1961-06-30 563.290039 533.179443
7 AirPassengers 1961-07-31 553.620056 548.205322
8 AirPassengers 1961-08-31 514.540039 482.283997
9 AirPassengers 1961-09-30 476.270050 436.766449
10 AirPassengers 1961-10-31 454.630066 410.485748
11 AirPassengers 1961-11-30 485.720062 448.050140
XGBRegressor
0 435.160187
1 416.029083
2 448.230713
3 445.395935
4 445.133881
5 492.995789
6 537.146912
7 525.498474
8 486.249084
9 444.600647
10 403.147552
11 440.389496
Model: RandomForestRegressor
MAE: 29.460004170735676
MAPE: 0.06273562629706837
MSE: 1312.615479398286
RMSE: 36.230035597529934
R2: 0.7630432238413292
------------------------------
Model: LGBMRegressor
MAE: 33.18512725830078
MAPE: 0.06642671851348535
MSE: 1521.8363902389538
RMSE: 39.01072147806233
R2: 0.7252741183295524
------------------------------
Model: XGBRegressor
MAE: 31.828025817871094
MAPE: 0.06228239920466334
MSE: 1600.5113431926973
RMSE: 40.006391279303074
R2: 0.7110715102474809
------------------------------
ハイパーパラメータ調整をする
先ほど説明したGridSearchCVによる「ハイパーパラメータ調整」の方法を組み合わせます。
GridSearchCVのインスタンスの名称が同じなので、名前を付ける(区別する)ために、モデルの一覧を辞書で定義し渡します。
以下、コードです。
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from mlforecast.lag_transforms import ExpandingMean, RollingMean
from sklearn.ensemble import RandomForestRegressor
from lightgbm import LGBMRegressor
from xgboost import XGBRegressor
from sklearn.model_selection import GridSearchCV, TimeSeriesSplit
# モデルの辞書形式
models = {
'rf_gscv': GridSearchCV(
estimator=RandomForestRegressor(random_state=42),
param_grid={
'n_estimators': [10, 50, 100, 200],
'max_depth': [2, 10, 20, None]
},
cv=TimeSeriesSplit(n_splits=5),
scoring='neg_mean_absolute_error',
),
'lgbm_gscv': GridSearchCV(
estimator=LGBMRegressor(random_state=42),
param_grid={
'n_estimators': [10, 50, 100, 200],
'num_leaves': [31, 40, 50]
},
cv=TimeSeriesSplit(n_splits=5),
scoring='neg_mean_absolute_error',
),
'xgb_gscv': GridSearchCV(
estimator=XGBRegressor(random_state=42),
param_grid={
'n_estimators': [10, 50, 100, 200],
'max_depth': [3, 6, 9]
},
cv=TimeSeriesSplit(n_splits=5),
scoring='neg_mean_absolute_error',
)
}
# MLForecastのインスタンスを作成
fcst = MLForecast(
models=models,
freq='M', # 月単位
lags=[1], # ラグ特徴量(過去1期)
lag_transforms={
1: [RollingMean(window_size=12)], #ローリング特徴量(前期までの過去12期移動平均)
1: [ExpandingMean()], #エクスパンディング特徴量(前期までの全期間平均)
},
target_transforms=[Differences([1])], # 差分処理(過去1期からの差分)
)
このコードの場合は、モデルの辞書を作成し、MLForecastのmodelsに設定しているだけです。
あとは、先ほどとほぼ同じコードで実施するため、まとめて記載します。前処理⇒学習⇒予測⇒精度評価と進みます。
以下、コードです。
# データの前処理
fcst.preprocess(
transformed_df, # 学習データ
static_features=[], # 静的特徴量(今回はなし)
dropna=True, # 欠損値の削除
)
# 学習
fcst.fit(
transformed_df,
static_features=[]
)
# 予測を行う(12か月先までの予測)
forecast = fcst.predict(
12, # 予測期間
X_df=future_df, # 予測期間の外生変数(今回は三角関数特徴量)
)
# 結果の表示
print(forecast)
from sklearn.metrics import (
mean_absolute_error, # MAE
mean_absolute_percentage_error, # MAPE
mean_squared_error, # MSE
r2_score, # R2
)
# 予測 'y' 列を使って評価指標を計算(文字列列を無視するため)
y_true = Y_test_df['y'].values
# 使用するモデルの名称リスト
model_names = ['rf_gscv', 'lgbm_gscv', 'xgb_gscv']
# 各モデルに対して評価指標を計算
for model_name in model_names:
# 予測結果を取得
y_pred = forecast[model_name].values
# 各指標を計算
mae = mean_absolute_error(y_true, y_pred) # MAEの計算
mape = mean_absolute_percentage_error(y_true, y_pred) # MAPEの計算
mse = mean_squared_error(y_true, y_pred) # MSEの計算
rmse = mean_squared_error(y_true, y_pred, squared=False) # RMSEの計算
r2 = r2_score(y_true, y_pred) # R2の計算
# 計算結果を表示
print(f"Model: {model_name}")
print('MAE:', mae)
print('MAPE:', mape)
print('MSE:', mse)
print('RMSE:', rmse)
print('R2:', r2)
print('\n' + '-'*30 + '\n')
以下、実行結果です。
unique_id ds rf_gscv lgbm_gscv xgb_gscv 0 AirPassengers 1960-12-31 436.440002 442.300018 433.333374 1 AirPassengers 1961-01-31 415.399994 425.104218 425.250702 2 AirPassengers 1961-02-28 446.539978 451.050629 445.081482 3 AirPassengers 1961-03-31 462.819977 461.283173 434.675018 4 AirPassengers 1961-04-30 465.199982 466.997101 442.289368 5 AirPassengers 1961-05-31 520.000000 527.882935 489.042328 6 AirPassengers 1961-06-30 567.820007 576.748962 531.376160 7 AirPassengers 1961-07-31 556.660034 578.415283 538.344971 8 AirPassengers 1961-08-31 517.880005 510.372375 497.703674 9 AirPassengers 1961-09-30 478.739990 461.873718 441.935883 10 AirPassengers 1961-10-31 451.359985 418.940277 410.493958 11 AirPassengers 1961-11-30 485.059998 451.002808 451.900696 Model: rf_gscv MAE: 28.37999216715495 MAPE: 0.06064630546069558 MSE: 1197.409423181399 RMSE: 34.60360419351428 R2: 0.7838405221389404 ------------------------------ Model: lgbm_gscv MAE: 18.990244547526043 MAPE: 0.040994464895061346 MSE: 576.6503395017547 RMSE: 24.0135449174368 R2: 0.8959015739462586 ------------------------------ Model: xgb_gscv MAE: 33.89106750488281 MAPE: 0.06771188732876487 MSE: 1656.9454715273653 RMSE: 40.705595088726625 R2: 0.700883873940131 ------------------------------
まとめ
今回は、mlforecastを活用したテーブルデータ系の機械学習モデルによる時系列予測について説明しました。
複数のモデル構築とハイパーパラメータ調整の実践方法や、Scikit-learnのGridSearchCVを用いた効率的なモデル調整手法や複数モデルによる予測などを解説しました。
mlforecastには、ラグ特徴量やローリング特徴量などの時系列特徴量を作成できる機能が備わっているため、非常にテーブルデータ系の数理モデルで予測モデルを構築するときに、非常に便利です。
Python mlforecast で始める 機械学習 時系列予測 入門– 第3回:mlforecastの時系列特徴量と目的変数変換 –

