第1回では prince ライブラリでコレスポンデンス分析のマップを描き、第2回では「期待度数からのズレ(残差)」がその出発点であることを学びました。
しかし、「残差の表」から「2次元マップの座標」がどうやって生まれるのかを、まだ説明していません。
今回はこの謎を解き明かします。
鍵となるのが特異値分解(SVD: Singular Value Decomposition)という行列分解の手法です。
「行列分解」と聞くと身構えてしまうかもしれませんが、安心してください。
一つひとつのステップをPythonで確かめながら進めるので、最終的には「なるほど、こうやって座標が決まるのか」と腑に落ちるはずです(たぶん)。
Contents
ライブラリとデータ
おなじみのセットアップです。
以下、コードです。前回までと同じライブラリです。
import numpy as np import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import japanize_matplotlib import prince
以下、コードです。前回までと同様のクロス集計表です。
# おなじみのクロス集計表
data = {
'カレー': [45, 30, 25, 35],
'ラーメン': [40, 25, 20, 30],
'パスタ': [20, 35, 40, 25],
'定食': [35, 30, 25, 40],
'サラダ': [10, 30, 40, 20]
}
index = ['工学部', '経済学部', '文学部', '理学部']
cross_table = pd.DataFrame(data, index=index)
print("【クロス集計表】")
print(cross_table)
以下、実行結果です。
【クロス集計表】
カレー ラーメン パスタ 定食 サラダ
工学部 45 40 20 35 10
経済学部 30 25 35 30 30
文学部 25 20 40 25 40
理学部 35 30 25 40 20
以降では、このクロス集計表を F と書きます。F は I 行 J 列の行列で、今回のデータでは I = 4(学部数)、J = 5(メニュー数)です。
F の (i, j) 要素 f_{ij} は「学部 i でメニュー j を選んだ人数」を表します。また、全体の人数(総度数)を n = \sum_{i}\sum_{j} f_{ij} と書きます。今回のデータでは n = 600 です。
① 対応行列:まず「割合」に変換する
クロス集計表 F の生の数値(45人、30人……)は、サンプルサイズ n に依存します。
もし600人ではなく6000人にアンケートを取っていたら、すべての数値が10倍になりますが、学部とメニューの「関係性」自体は変わらないはずです。
この影響を取り除くために、まず n で割って相対度数に変換します。
これを対応行列(correspondence matrix)と呼び、記号 P で表します。
$$
P = \frac{1}{n} F
$$
$$
p_{ij} = \frac{f_{ij}}{n}
$$
すべての要素を足し合わせると \sum_{i}\sum_{j} p_{ij} = 1 になります。
以下、コードです。
# 総度数 n
grand_total = cross_table.values.sum()
# 対応行列 P = F / n
P = cross_table / grand_total
print("【対応行列 P(相対度数)】")
print(P.round(4))
print(
"\n全要素の和: "
f"{P.values.sum():.4f}"
)
以下、実行結果です。
【対応行列 P(相対度数)】
カレー ラーメン パスタ 定食 サラダ
工学部 0.0750 0.0667 0.0333 0.0583 0.0167
経済学部 0.0500 0.0417 0.0583 0.0500 0.0500
文学部 0.0417 0.0333 0.0667 0.0417 0.0667
理学部 0.0583 0.0500 0.0417 0.0667 0.0333
全要素の和: 1.0000
すべての要素を足すとぴったり1になることを確認してください。
たとえば左上の値は「全600人のうち、工学部でカレーを選んだ人の割合」です。
② 周辺確率とプロファイル
周辺確率:行と列の「重み」
対応行列 P から、行と列それぞれの合計を計算します。これを周辺確率と呼びます。
行の周辺確率 r_i は、対応行列の第 i 行をすべて足し合わせたもので、「全データに占める学部 i の割合」を意味します。
$$
r_i = \sum_{j=1}^{J} p_{ij}
$$
たとえば工学部なら r_{\text{工学部}} = 0.075 + 0.067 + 0.033 + 0.058 + 0.017 = 0.25 です。
これは「全体の25%が工学部の学生」ということを表しています。
列の周辺確率 c_j は、対応行列の第 j 列をすべて足し合わせたもので、「全データに占めるメニュー j の割合」を意味します。
$$
c_j = \sum_{i=1}^{I} p_{ij}
$$
Pythonで計算してみましょう。
以下、コードです。
# 行の周辺確率 r(各学部の割合)
r = P.sum(axis=1)
# 列の周辺確率 c(各メニューの割合)
c = P.sum(axis=0)
print("【行の周辺確率 r】")
for faculty, prob in r.items():
print(f" {faculty}: {prob:.4f}")
print("\n【列の周辺確率 c】")
for menu, prob in c.items():
print(f" {menu}: {prob:.4f}")
以下、実行結果です。
【行の周辺確率 r】 工学部: 0.2500 経済学部: 0.2500 文学部: 0.2500 理学部: 0.2500 【列の周辺確率 c】 カレー: 0.2250 ラーメン: 0.1917 パスタ: 0.2000 定食: 0.2167 サラダ: 0.1667
周辺確率は、後のステップで「重みづけ」として繰り返し登場します。
サンプルの多いカテゴリほど周辺確率が大きくなり、分析への影響力も大きくなります。
行プロファイル:「その学部の中での」メニュー分布
行プロファイルは、各行(学部)の中でメニューがどんな比率で選ばれたかを表す分布です。
対応行列の各要素をその行の周辺確率 r_i で割ることで求まります。
$$
a_{ij} = \frac{p_{ij}}{r_i}
$$
ここで a_{ij} は「学部 i の学生のうち、メニュー j を選んだ人の比率」です。
各行の要素を足すと \sum_{j} a_{ij} = 1 になります。
たとえば工学部(r_i = 0.25)のカレー(p_{ij} = 0.075)なら、a_{ij} = 0.075 / 0.25 = 0.30 です。
つまり「工学部の学生の30%がカレーを選んだ」という意味になります。
以下、コードです。
# 行プロファイル:各行を行の周辺確率で割る
row_profiles = cross_table.div(
cross_table.sum(axis=1),
axis=0
)
print("【行プロファイル(各学部内のメニュー比率)】")
print(row_profiles.round(4))
以下、実行結果です。
【行プロファイル(各学部内のメニュー比率)】
カレー ラーメン パスタ 定食 サラダ
工学部 0.3000 0.2667 0.1333 0.2333 0.0667
経済学部 0.2000 0.1667 0.2333 0.2000 0.2000
文学部 0.1667 0.1333 0.2667 0.1667 0.2667
理学部 0.2333 0.2000 0.1667 0.2667 0.1333
この行プロファイルこそが、コレスポンデンス分析マップで各学部の「位置」を決める元になる情報です。
もし2つの学部の行プロファイルが似ていれば(=メニューの選び方が似ていれば)、マップ上でも近くにプロットされます。
列プロファイル:「そのメニューを選んだ」学部の分布
同様に、列プロファイルは各列(メニュー)の中で学部がどんな比率を占めるかを表します。
対応行列の各要素をその列の周辺確率 c_j で割って求めます。
$$
b_{ij} = \frac{p_{ij}}{c_j}
$$
ここで b_{ij} は「メニュー j を選んだ学生のうち、学部 i に所属している人の比率」です。
各列の要素を足すと \sum_{i} b_{ij} = 1 になります。
以下、コードです。
# 列プロファイル:各列を列の周辺確率で割る
col_profiles = cross_table.div(
cross_table.sum(axis=0),
axis=1
)
print("【列プロファイル(各メニューを選んだ学部の比率)】")
print(col_profiles.round(4))
以下、実行結果です。
【列プロファイル(各メニューを選んだ学部の比率)】
カレー ラーメン パスタ 定食 サラダ
工学部 0.3333 0.3478 0.1667 0.2692 0.1
経済学部 0.2222 0.2174 0.2917 0.2308 0.3
文学部 0.1852 0.1739 0.3333 0.1923 0.4
理学部 0.2593 0.2609 0.2083 0.3077 0.2
行プロファイルと列プロファイルは、それぞれ「行方向から見た分布」「列方向から見た分布」を表しています。
コレスポンデンス分析はこの両方の情報を使って、行と列のカテゴリを同じ空間に配置します。
③ 標準化残差行列:SVDにかける行列を作る
第2回で「標準化残差」を計算したのを覚えていますか?
あのときは期待度数の平方根で割りましたが、今回は対応行列ベースの表現で書き直します。
やっていることは本質的に同じですが、こちらの形のほうがSVDとの接続がスムーズです。
もし学部とメニュー選択が完全に独立であれば、対応行列の (i, j) 要素は r_i \cdot c_j(行と列の周辺確率の積)になるはずでした。
実際の値 p_{ij} との差 p_{ij} - r_i c_j が「独立からのズレ」です。
標準化残差行列 S の (i, j) 要素 s_{ij} は、このズレを \sqrt{r_i \cdot c_j} で割って標準化したものです。
$$
s_{ij} = \frac{p_{ij} – r_i \cdot c_j}{\sqrt{r_i \cdot c_j}}
$$
分子の p_{ij} - r_i c_j は相対度数ベースの残差で、正ならその組み合わせが「期待より多い」、負なら「期待より少ない」ことを意味します。
分母の \sqrt{r_i c_j} は、周辺確率が小さい(サンプルが少ない)セルの残差が過大評価されないように調整する役割を果たします。
以下、コードです。
# 周辺確率をNumPy配列で取得
r_vals = r.values # 行の周辺確率のベクトル(長さ I)
c_vals = c.values # 列の周辺確率のベクトル(長さ J)
# 期待確率行列(独立の場合の理論値)
# np.outer で r と c のすべての組み合わせ r_i * c_j を計算
expected_P = np.outer(r_vals, c_vals)
# 標準化残差行列 S
S = (
(P.values - expected_P)
/ np.sqrt(expected_P)
)
S_df = pd.DataFrame(
S,
index=cross_table.index,
columns=cross_table.columns
)
print("【標準化残差行列 S】")
print(S_df.round(4))
以下、実行結果です。
【標準化残差行列 S】
カレー ラーメン パスタ 定食 サラダ
工学部 0.0791 0.0857 -0.0745 0.0179 -0.1225
経済学部 -0.0264 -0.0286 0.0373 -0.0179 0.0408
文学部 -0.0615 -0.0666 0.0745 -0.0537 0.1225
理学部 0.0088 0.0095 -0.0373 0.0537 -0.0408
第2回のヒートマップで見た「赤いセル(正)・青いセル(負)」のパターンが、ここでも数値として確認できるはずです。
この I \times J の行列 S が、次のステップでSVDにかけられる「主役」です。
④ 特異値分解(SVD):行列を3つに分解する
SVDとは何か ― 直感的なイメージ
いよいよ今回のメインテーマです。特異値分解(SVD)は、任意の I \times J 行列を3つの行列の積に分解する手法です。
標準化残差行列 S に適用すると、次のように書けます。
$$
S = U \Sigma V^T
$$
ここで登場する3つの行列の意味は次の通りです。
U は I \times K の行列で、左特異ベクトルと呼ばれます。各列が一つの「成分(パターン)」に対応し、行(学部)がその成分にどう関わっているかを表します。K = \min(I, J) で、今回は K = \min(4, 5) = 4 です。 \Sigma(シグマ)は K \times K の対角行列で、対角要素 \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_K \geq 0 を特異値と呼びます。特異値は各成分の「重要度」を表し、大きい順に並んでいます。 V^T は K \times J の行列で、V の各列が右特異ベクトルです。列(メニュー)が各成分にどう関わっているかを表します。直感的には、SVDは「複雑なデータの変動パターンを、重要度の高い順にランク付けして分解する」操作です。
写真の圧縮に例えると、高解像度の写真を「最も重要な特徴」「2番目に重要な特徴」……と分解し、上位の数個だけ残しても元の写真にかなり近いものが復元できる、というイメージです。
Pythonで実行する
NumPyの np.linalg.svd() を使えば、1行でSVDを実行できます。
以下、コードです。
# S = U @ diag(singular_values) @ Vt
U, singular_values, Vt = np.linalg.svd(
S,
full_matrices=False
)
print(f"U の形状: {U.shape} (I × K = 学部数 × 成分数)")
print(f"Σ の形状: {singular_values.shape} (特異値の数)")
print(f"Vt の形状: {Vt.shape} (K × J = 成分数 × メニュー数)")
以下、実行結果です。
U の形状: (4, 4) (I × K = 学部数 × 成分数) Σ の形状: (4,) (特異値の数) Vt の形状: (4, 5) (K × J = 成分数 × メニュー数)
np.linalg.svd は \Sigma を対角行列ではなく1次元配列(特異値だけのベクトル)として返す点に注意してください。Vt は V^T(V の転置)です。
特異値を確認する
特異値 \sigma_k は「第 k 成分がデータの変動をどれだけ捉えているか」を表すスカラー値で、大きい順に並んでいます。
以下、コードです。
print("【特異値 σ】")
for i, sv in enumerate(singular_values):
print(f" σ{i+1} = {sv:.4f}")
以下、実行結果です。
【特異値 σ】 σ1 = 0.2717 σ2 = 0.0563 σ3 = 0.0111 σ4 = 0.0000
第1成分の特異値が最も大きく、後ろにいくほど小さくなります。
コレスポンデンス分析の2次元マップでは、上位2つの成分だけを使います。
寄与率:各成分がどれだけ「説明」しているか
特異値の二乗 \sigma_k^2 は、第 k 成分の固有値(=イナーシャ)で、その成分が説明するデータの変動量に対応します。
すべての成分のイナーシャを足し合わせたものが総イナーシャです。
$$
\lambda_k = \sigma_k^2, \qquad \text{総イナーシャ} = \sum_{k=1}^{K} \lambda_k
$$
第2回で学んだように、総イナーシャは \chi^2 / n と一致します。
各成分の寄与率は、その成分のイナーシャが総イナーシャに占める割合です。
$$
\text{第 } k \text{ 成分の寄与率} = \frac{\lambda_k}{\sum_{k’} \lambda_{k’}} = \frac{\sigma_k^2}{\sum_{k’} \sigma_{k’}^2}
$$
以下、コードです。
# 特異値の二乗 = 各成分のイナーシャ(固有値)
inertia = singular_values ** 2
total_inertia = inertia.sum()
explained_ratio = inertia / total_inertia
print("【各成分の寄与率】")
cumulative = 0
for i in range(len(inertia)):
cumulative += explained_ratio[i]
print(
f" 第{i+1}成分: λ={inertia[i]:.4f}, "
f"寄与率={explained_ratio[i]*100:.1f}%, "
f"累積={cumulative*100:.1f}%"
)
print(f"\n総イナーシャ: {total_inertia:.4f}")
以下、実行結果です。
【各成分の寄与率】 第1成分: λ=0.0738, 寄与率=95.7%, 累積=95.7% 第2成分: λ=0.0032, 寄与率=4.1%, 累積=99.8% 第3成分: λ=0.0001, 寄与率=0.2%, 累積=100.0% 第4成分: λ=0.0000, 寄与率=0.0%, 累積=100.0% 総イナーシャ: 0.0771
第1成分と第2成分の累積寄与率が70%を超えていれば、2次元マップでデータの変動を十分に要約できていると判断できます。
この寄与率は、第1回で prince が返していた数字そのものです。
⑤ 行座標と列座標を計算する
SVDで得られた U, \Sigma, V^T を使って、行(学部)と列(メニュー)のマップ上の座標を計算します。ここが最後のピースです。
ただし、SVDの出力をそのまま座標にするわけではありません。周辺確率による重みづけが必要です。
なぜかというと、標準化残差行列 S を作る際に \sqrt{r_i c_j} で割っているため、周辺確率が小さいカテゴリほど S の値が膨らみやすくなっています。
座標を計算する際にこの影響を戻してやる必要があるのです。
具体的には、D_r^{-1/2} と D_c^{-1/2} という対角行列を使います。
D_r^{-1/2} は対角要素に 1/\sqrt{r_i} を並べた I \times I の対角行列、D_c^{-1/2} は対角要素に 1/\sqrt{c_j} を並べた J \times J の対角行列です。行座標(学部のマップ上の位置)は次の式で計算します。
$$
\text{行座標} = D_r^{-1/2} \cdot U \cdot \Sigma
$$
第 k 成分における行 i の座標を \phi_{ik} と書くと、次のようになります。
$$
\phi_{ik} = \frac{1}{\sqrt{r_i}} \cdot u_{ik} \cdot \sigma_k
$$
ここで u_{ik} は U の (i, k) 要素、\sigma_k は第 k 特異値です。1/\sqrt{r_i} の部分が周辺確率による重みづけで、サンプルの少ない学部の座標を適切に補正しています。
以下、コードです。
# 行座標の計算
# 対角行列 D_r^{-1/2}
Dr_inv_sqrt = np.diag(1 / np.sqrt(r_vals))
# D_r^{-1/2} × U × Σ
row_coords = Dr_inv_sqrt @ U * singular_values
row_coords_df = pd.DataFrame(
row_coords[:, :2], # 上位2成分だけ取り出す
index=cross_table.index,
columns=['次元1', '次元2']
)
print("【行座標(学部)-- 手計算】")
print(row_coords_df.round(4))
以下、実行結果です。
【行座標(学部)-- 手計算】
次元1 次元2
工学部 0.3665 -0.0595
経済学部 -0.1385 -0.0050
文学部 -0.3547 -0.0269
理学部 0.1267 0.0914
列座標(メニューのマップ上の位置)も同様に計算します。
$$
\text{列座標} = D_c^{-1/2} \cdot V \cdot \Sigma
$$
第 k 成分における列 j の座標を \gamma_{jk} と書くと、次のようになります。
$$
\gamma_{jk} = \frac{1}{\sqrt{c_j}} \cdot v_{jk} \cdot \sigma_k
$$
ここで v_{jk} は V の (j, k) 要素です。np.linalg.svd が返すのは V^T(転置済み)なので、V を得るには転置する必要があります。
以下、コードです。
# 列座標の計算
# 対角行列 D_c^{-1/2}
Dc_inv_sqrt = np.diag(1 / np.sqrt(c_vals))
# D_c^{-1/2} × V × Σ
col_coords = Dc_inv_sqrt @ Vt.T * singular_values
col_coords_df = pd.DataFrame(
col_coords[:, :2], # 上位2成分だけ取り出す
index=cross_table.columns,
columns=['次元1', '次元2']
)
print("【列座標(メニュー)-- 手計算】")
print(col_coords_df.round(4))
以下、実行結果です。
【列座標(メニュー)-- 手計算】
次元1 次元2
カレー 0.2155 -0.0397
ラーメン 0.2529 -0.0466
パスタ -0.2618 -0.0231
定食 0.1379 0.1027
サラダ -0.4469 0.0013
これで、各学部と各メニューに2つの座標値が割り当てられました。
この座標をそのまま散布図にプロットすれば、コレスポンデンス分析のマップになります。
答え合わせ:prince の結果と比較する
ここまでの手計算が正しいかどうか、prince ライブラリの出力と突き合わせてみましょう。
以下、コードです。
ca = prince.CA(n_components=2, random_state=42)
ca = ca.fit(cross_table)
prince_row = ca.row_coordinates(cross_table)
prince_col = ca.column_coordinates(cross_table)
print("【行座標の比較】")
print("prince:")
print(prince_row.round(4).to_string())
print("\n手計算:")
print(row_coords_df.round(4).to_string())
print()
print("【列座標の比較】")
print("prince:")
print(prince_col.round(4).to_string())
print("\n手計算:")
print(col_coords_df.round(4).to_string())
以下、実行結果です。
【行座標の比較】
prince:
0 1
工学部 0.3665 -0.0595
経済学部 -0.1385 -0.0050
文学部 -0.3547 -0.0269
理学部 0.1267 0.0914
手計算:
次元1 次元2
工学部 0.3665 -0.0595
経済学部 -0.1385 -0.0050
文学部 -0.3547 -0.0269
理学部 0.1267 0.0914
【列座標の比較】
prince:
0 1
カレー 0.2155 -0.0397
ラーメン 0.2529 -0.0466
パスタ -0.2618 -0.0231
定食 0.1379 0.1027
サラダ -0.4469 0.0013
手計算:
次元1 次元2
カレー 0.2155 -0.0397
ラーメン 0.2529 -0.0466
パスタ -0.2618 -0.0231
定食 0.1379 0.1027
サラダ -0.4469 0.0013
値が一致(または符号が反転しただけで絶対値が一致)していれば成功です。
仮にプラスマイナスの符号の反転があっても、SVDでは特異ベクトルの向き(正負)に数学的な任意性があるために起こるもので、問題ありません。
マップ上では点の相対的な位置関係が重要であり、軸の正負の向き自体には意味がないためです。
手計算の座標でマップを描く
最後に、手計算で得た座標を使ってコレスポンデンス分析マップを描き、第1回のマップと同じものが再現できることを確かめましょう。
以下、コードです。
fig, ax = plt.subplots(figsize=(10, 8))
# 学部をプロット(青い丸)
for i, faculty in enumerate(cross_table.index):
x, y = row_coords_df.iloc[i]
ax.scatter(x, y, s=200, c='#2E86AB', edgecolors='white',
linewidths=2, zorder=5)
ax.annotate(faculty, (x, y), fontsize=13, fontweight='bold',
xytext=(10, 10), textcoords='offset points',
color='#2E86AB')
# メニューをプロット(赤い三角)
for i, menu in enumerate(cross_table.columns):
x, y = col_coords_df.iloc[i]
ax.scatter(x, y, s=200, c='#E94F37', marker='^',
edgecolors='white', linewidths=2, zorder=5)
ax.annotate(menu, (x, y), fontsize=13, fontweight='bold',
xytext=(10, 10), textcoords='offset points',
color='#E94F37')
# 原点の十字線
ax.axhline(y=0, color='gray', linestyle='--', linewidth=0.8)
ax.axvline(x=0, color='gray', linestyle='--', linewidth=0.8)
# 軸ラベルに寄与率を表示
ax.set_xlabel(f'次元1(寄与率: {explained_ratio[0]*100:.1f}%)', fontsize=12)
ax.set_ylabel(f'次元2(寄与率: {explained_ratio[1]*100:.1f}%)', fontsize=12)
ax.set_title('コレスポンデンス分析マップ(手計算による再現)', fontsize=14)
# 凡例
from matplotlib.lines import Line2D
legend_elements = [
Line2D([0], [0], marker='o', color='w', markerfacecolor='#2E86AB',
markersize=12, label='学部'),
Line2D([0], [0], marker='^', color='w', markerfacecolor='#E94F37',
markersize=12, label='メニュー')
]
ax.legend(handles=legend_elements, fontsize=12, loc='best')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
以下、実行結果です。
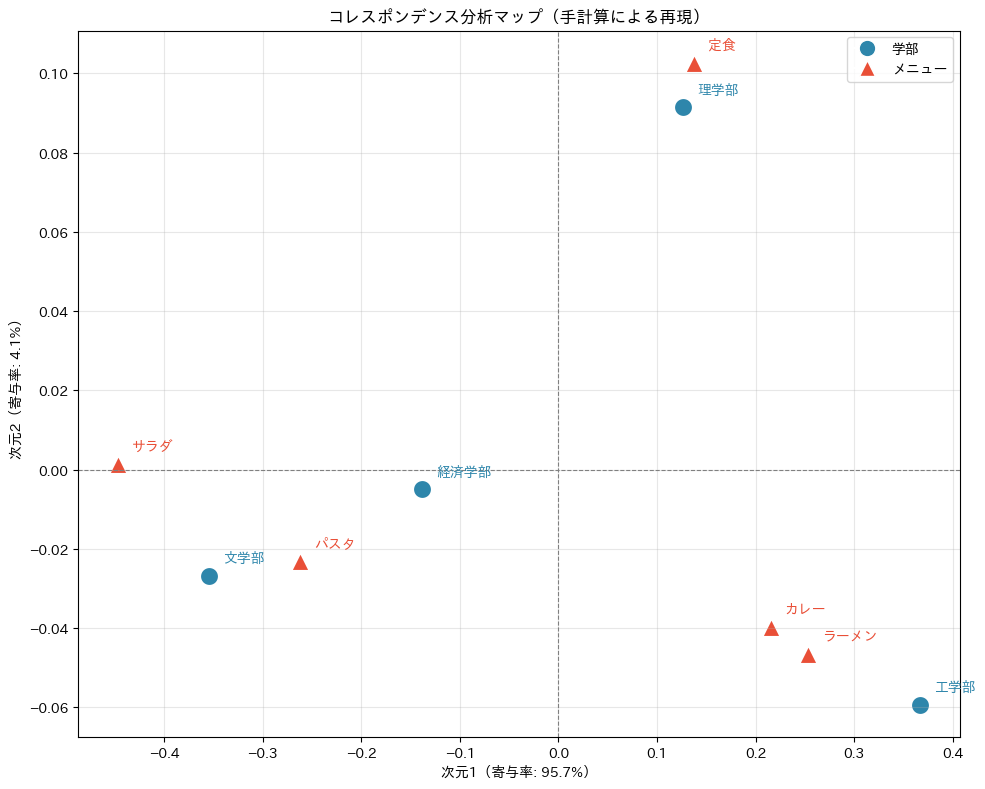
第1回で prince に任せて描いたマップと、ほぼ同じ構造のマップが手計算で再現できたはずです(たぶん)。
全体の流れを振り返る
今回たどったステップを、記号と数式で整理しておきましょう。
| ステップ | やること | 数式 |
|---|---|---|
| ① 対応行列 | クロス集計表 F を総度数 n で割る | p_{ij} = f_{ij} / n |
| ② 周辺確率 | 行・列の合計を求める | r_i = \sum_j p_{ij}, c_j = \sum_i p_{ij} |
| ② プロファイル | 行・列内の比率分布を求める | a_{ij} = p_{ij}/r_i, b_{ij} = p_{ij}/c_j |
| ③ 標準化残差 | 独立からのズレを標準化する | s_{ij} = (p_{ij} - r_i c_j) / \sqrt{r_i c_j} |
| ④ SVD | 行列 S を3つに分解する | S = U \Sigma V^T |
| ④ 寄与率 | 各成分の説明力を求める | \lambda_k / \sum_{k'} \lambda_{k'}(\lambda_k = \sigma_k^2) |
| ⑤ 行座標 | \phi_{ik} = u_{ik} \sigma_k / \sqrt{r_i} | |
| ⑤ 列座標 | 同上 | \gamma_{jk} = v_{jk} \sigma_k / \sqrt{c_j} |
この8つの式が、コレスポンデンス分析の「中身」のすべてです。prince のような便利なライブラリは、まさにこの一連の計算を内部で実行しています。
まとめ
今回は、コレスポンデンス分析のブラックボックスを開けて、中で何が起きているかを一歩ずつ追いかけました。
対応行列 P とプロファイルについて。クロス集計表 F を総度数 n で割って相対度数に変換したものが対応行列です。各行・列内の比率分布であるプロファイル(a_{ij} = p_{ij}/r_i, b_{ij} = p_{ij}/c_j)が、マップ上の位置を決める基礎情報になります。プロファイルが似ているカテゴリは、マップ上でも近くに配置されます。
標準化残差行列 S について。第2回で学んだ「独立からのズレ」を s_{ij} = (p_{ij} - r_i c_j) / \sqrt{r_i c_j} として定式化したものです。この行列がSVDの入力であり、コレスポンデンス分析の核心です。
特異値分解(SVD)について。標準化残差行列を S = U \Sigma V^T の3つに分解する操作です。特異値 \sigma_k の二乗が各成分のイナーシャ \lambda_k であり、その比率が寄与率になります。上位2成分の累積寄与率が高ければ、2次元マップで十分にデータを要約できています。
座標の計算について。U と V に特異値 \sigma_k と周辺確率の重み 1/\sqrt{r_i}, 1/\sqrt{c_j} をかけることで、行座標 \phi_{ik} と列座標 \gamma_{jk} が得られます。この座標をプロットしたものが、第1回で描いたコレスポンデンス分析マップです。
ここまでの3回で、2つのカテゴリ変数を扱う「基本のコレスポンデンス分析(CA)」の仕組みをひと通り理解できました。
しかし、実務のアンケート調査などでは「性別」「年代」「好きなブランド」「購入チャネル」……と、カテゴリ変数が3つも4つも出てくることが珍しくありません。
次回の第4回では、3つ以上のカテゴリ変数を同時に分析する多重コレスポンデンス分析(MCA)を紹介します。指示行列(ダミー変数化)やBurt行列という新しい道具を学び、顧客セグメンテーションの事例でMCAの威力を体感しましょう。

