データサイエンスの世界では、欠損データは避けて通れない問題です。データが完全でないことは、分析の正確性や結果の信頼性に大きな影響を与える可能性があります。 しかし、欠損データを理解し、適切に対処することで、これらの課題を...
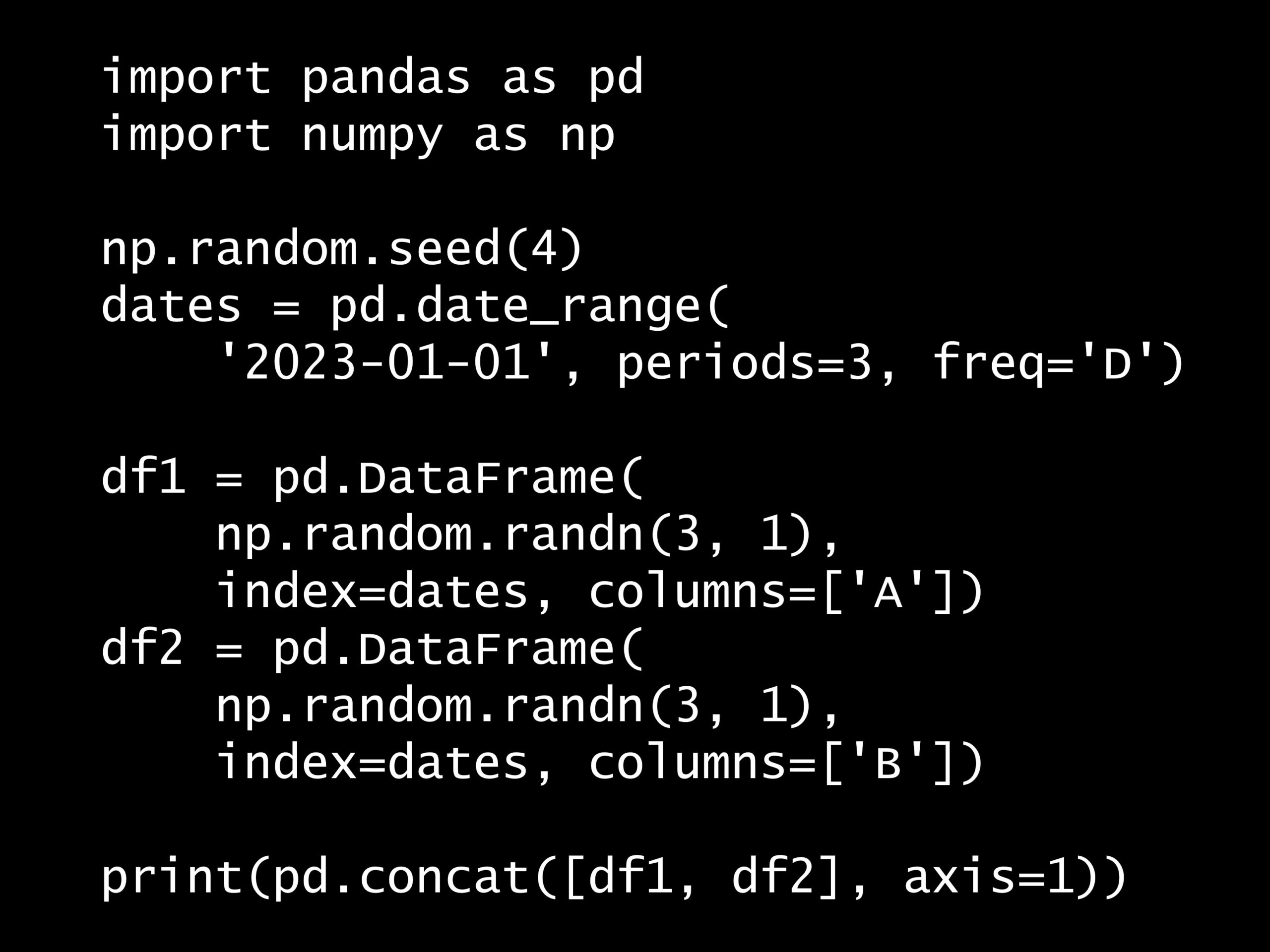
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd import numpy as np np.random.seed(4) dates = pd.date...
Pandasは、データ分析にPythonを使うデータサイエンティストにとって、最もよく使われているツールの1つです。 GPU データフレームのライブラリーの1つに、pandasライクなRAPIDS cuDF(cuda b...
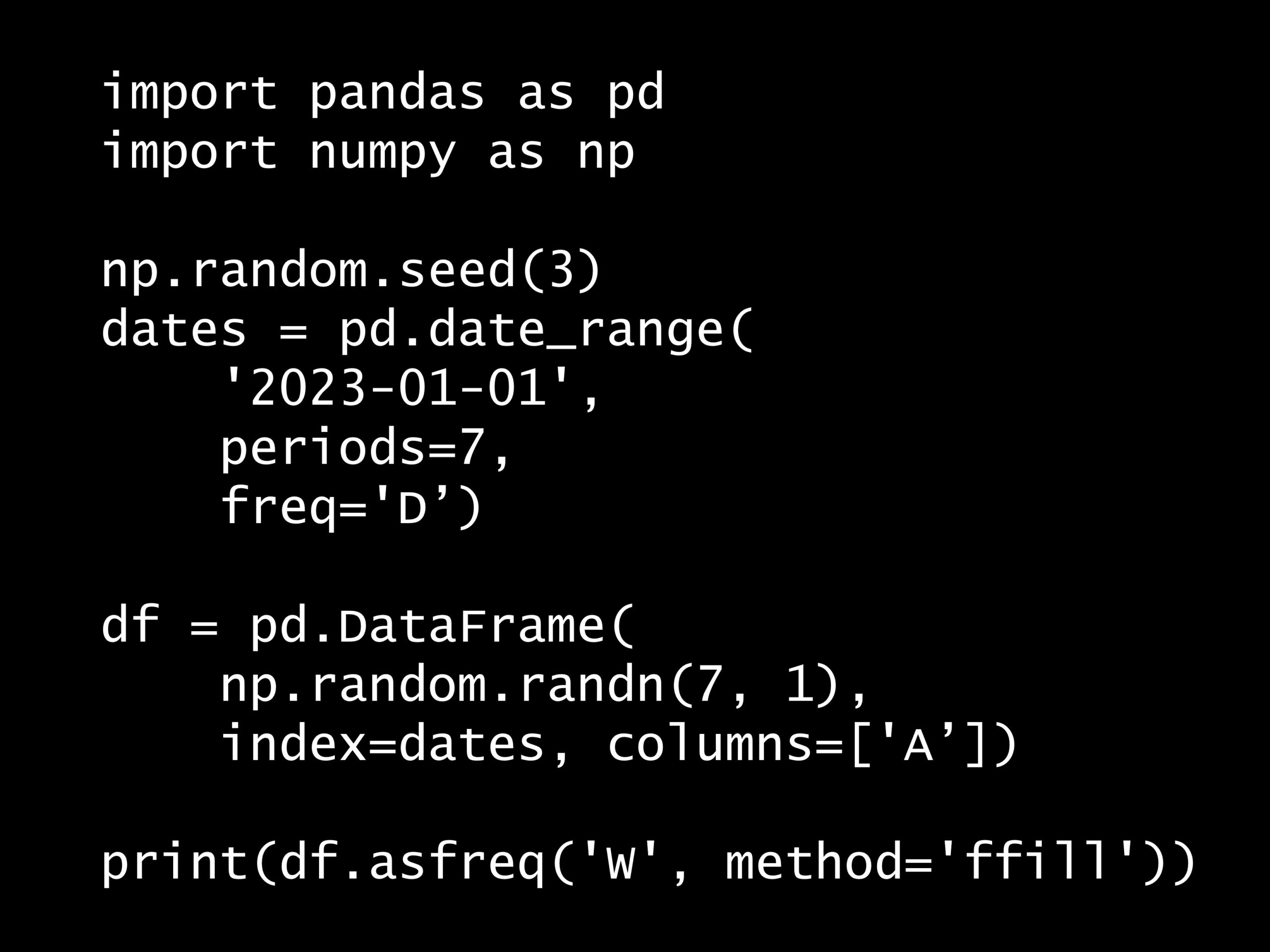
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd import numpy as np np.random.seed(3) dates = pd.date...
数理最適化と機械学習の融合は、ビジネスの意思決定に革命をもたらす可能性を秘めています。 具体的には、Scikit-learnで数理モデルを構築し、その数理モデルを目的変数としたSciPyを用い最適化問題を解きます。 例え...
Excelを使用する際、最小値を取得することがよくあります。このような場合に便利なのが、MIN関数です。 2007以降のバージョンに対応しています。 MIN関数を使用することで、手動で数値を比較する必要がなくなります。 ...
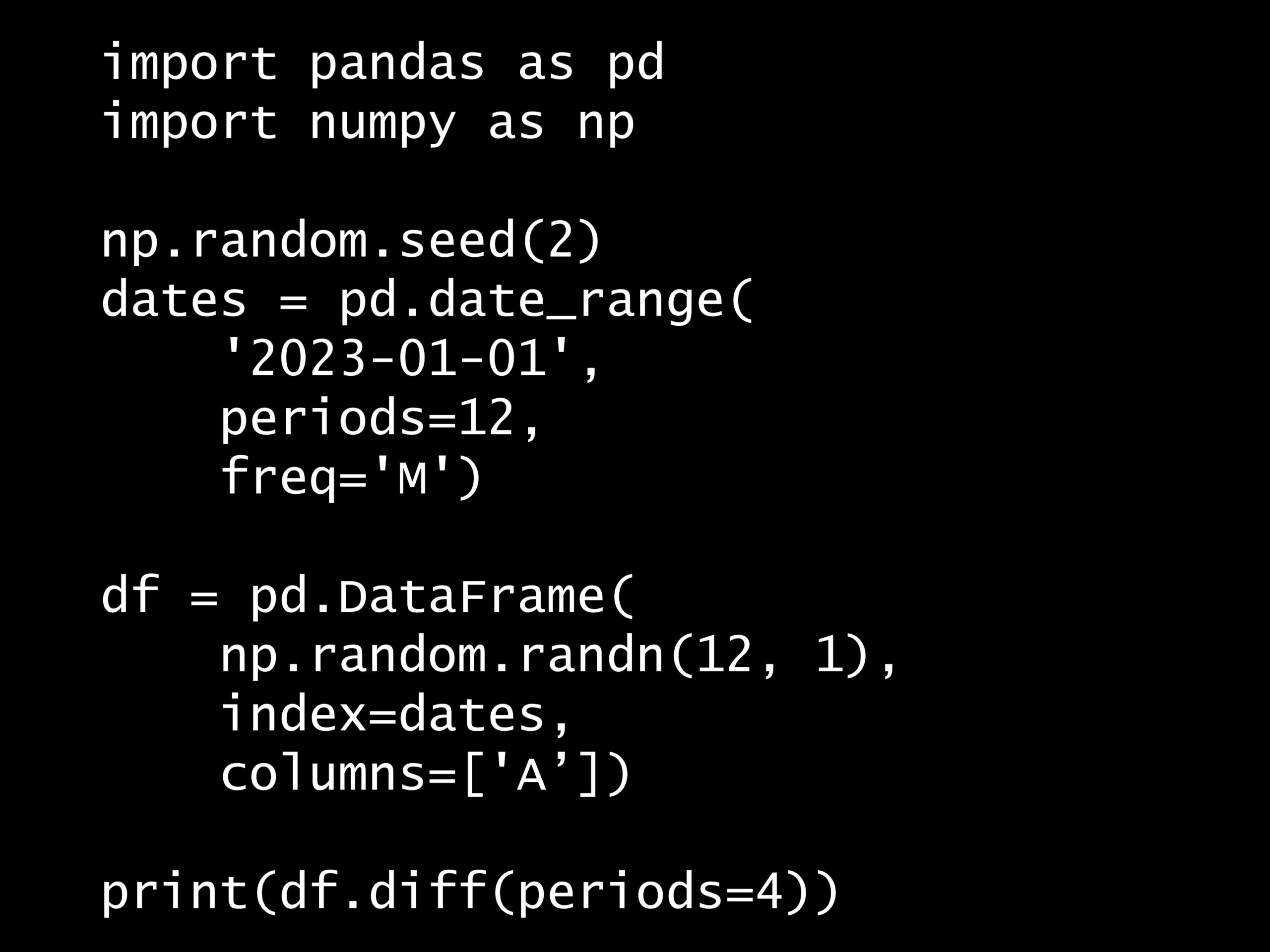
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd import numpy as np np.random.seed(2) dates = pd.date...
今回は、数理最適化のさらに高度な領域である「整数最適化」と「組合せ最適化」に焦点を当てます。 これらの最適化手法は、現実の複雑な問題を解決するために広く用いられています。 有名なところでは、巡回セールスマン問題やナップサ...
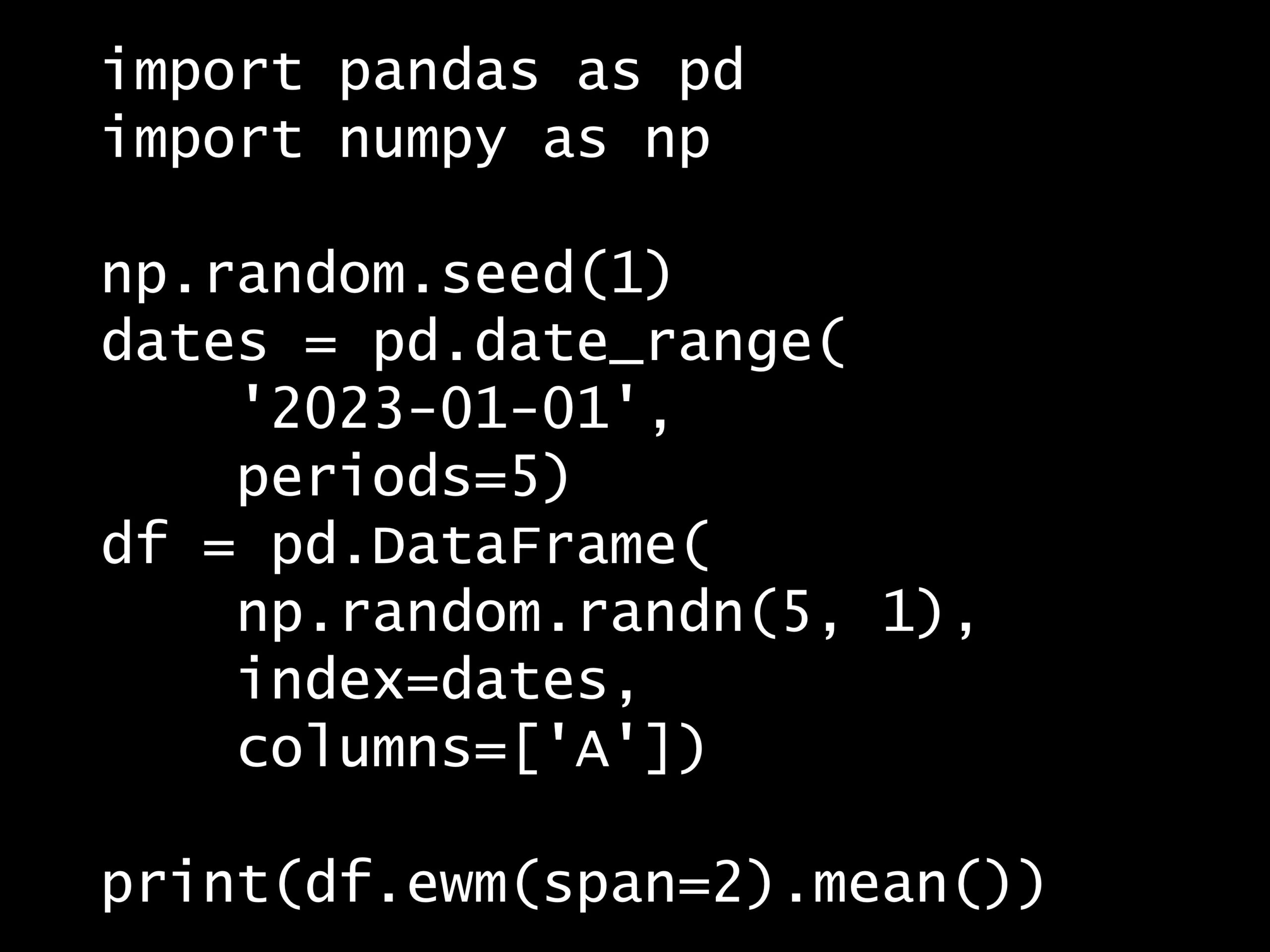
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd import numpy as np np.random.seed(1) dates = pd.date...
データは今日のビジネスの核心です。 しかし、この膨大なデータの海から有用な情報を引き出し、ビジネス戦略に活かすためには、高度な分析技術が必要とされます。ここで主役となるのが「主成分回帰(PCR)」です。 この技術は、複雑...
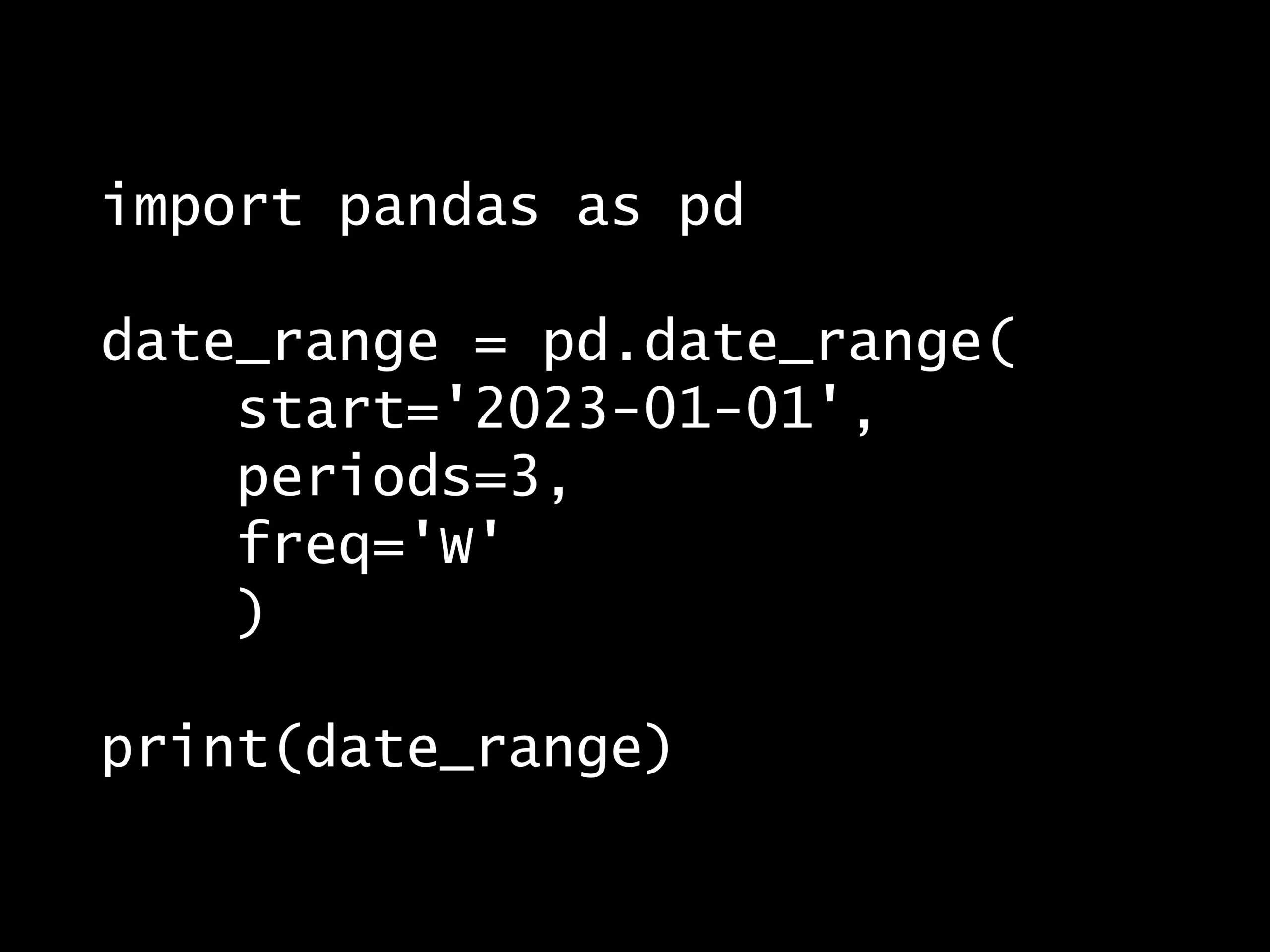
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd date_range = pd.date_range( start='2023-01-01', peri...
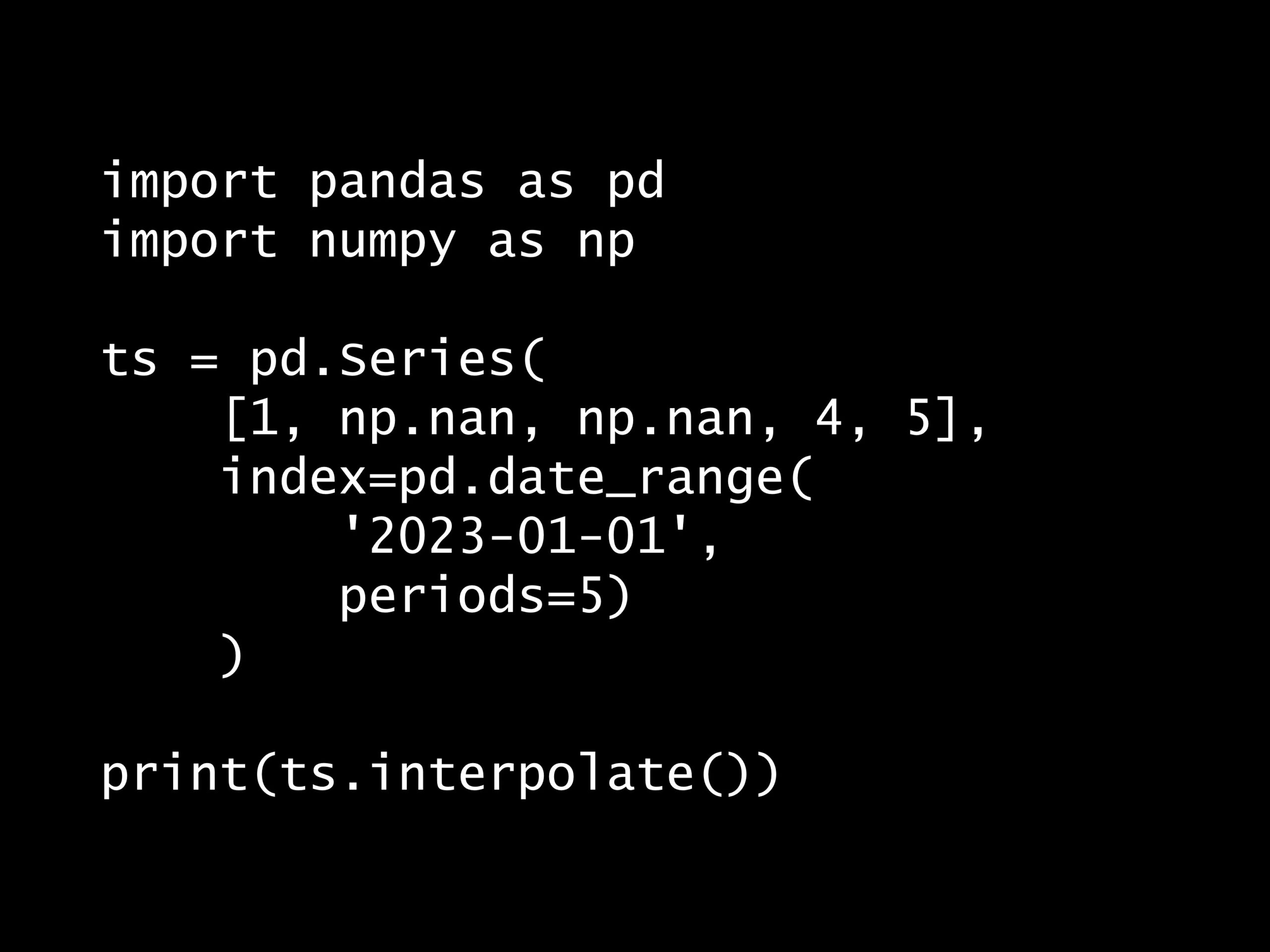
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd import numpy as np ts = pd.Series( [1, np.nan, n...
記事『【AVERAGE関数】使い方と解説 – 平均値 –』では、「AVERAGE関数」を紹介しました。 本記事は、AVERAGE関数を拡張させたAVERAGEIF関数を紹介します。 ちなみに、SUMIF関数の平均版がAV...
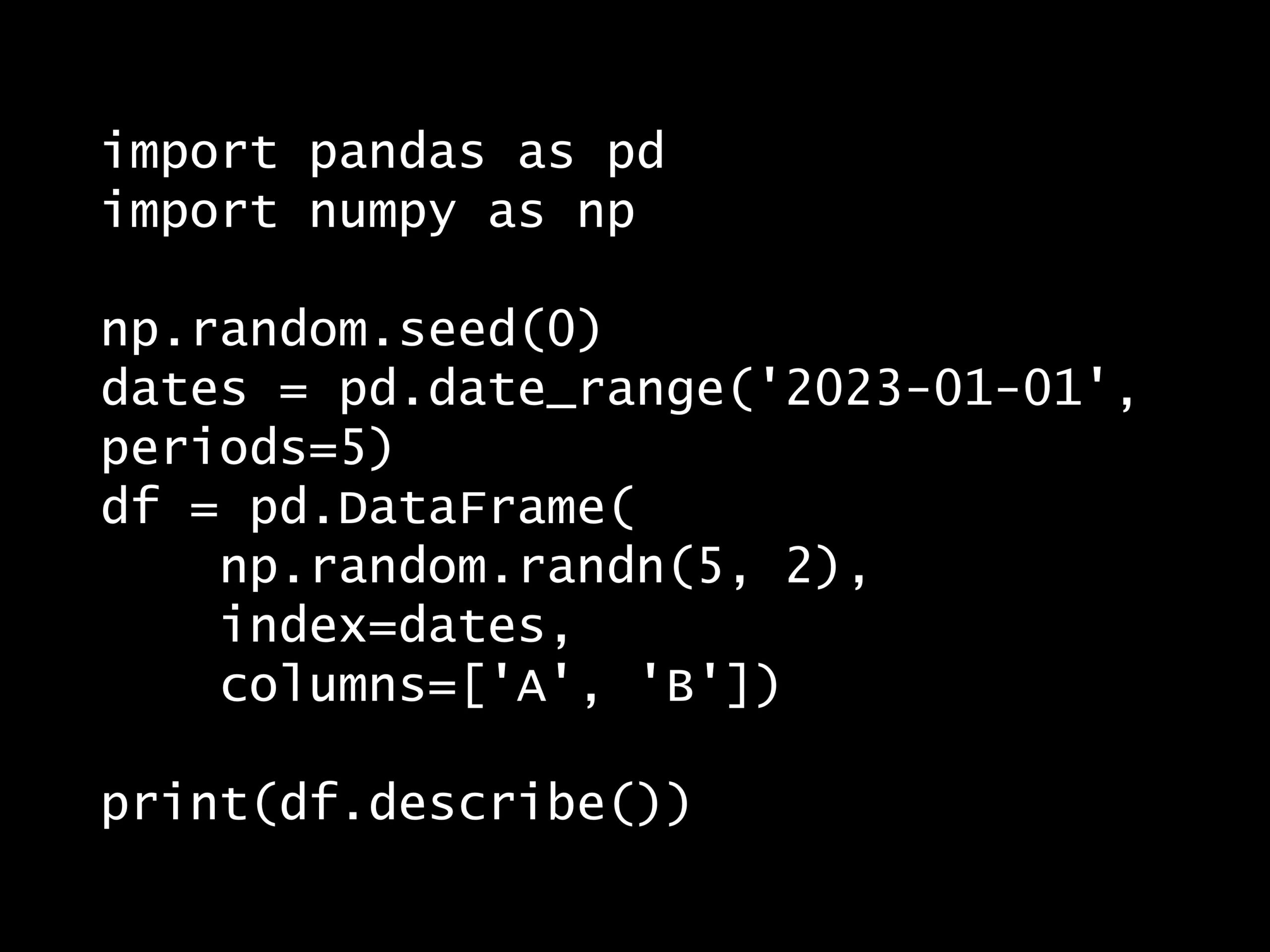
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd import numpy as np np.random.seed(0) dates = pd.date...
書籍や論文、Webサイトなどに記載されている、目の前の数式を LaTeX コードとして手に入れたい! と思った方も多いことでしょう。 私は結構あります。 Pythonのライブラリ pix2tex で実現できます。 という...
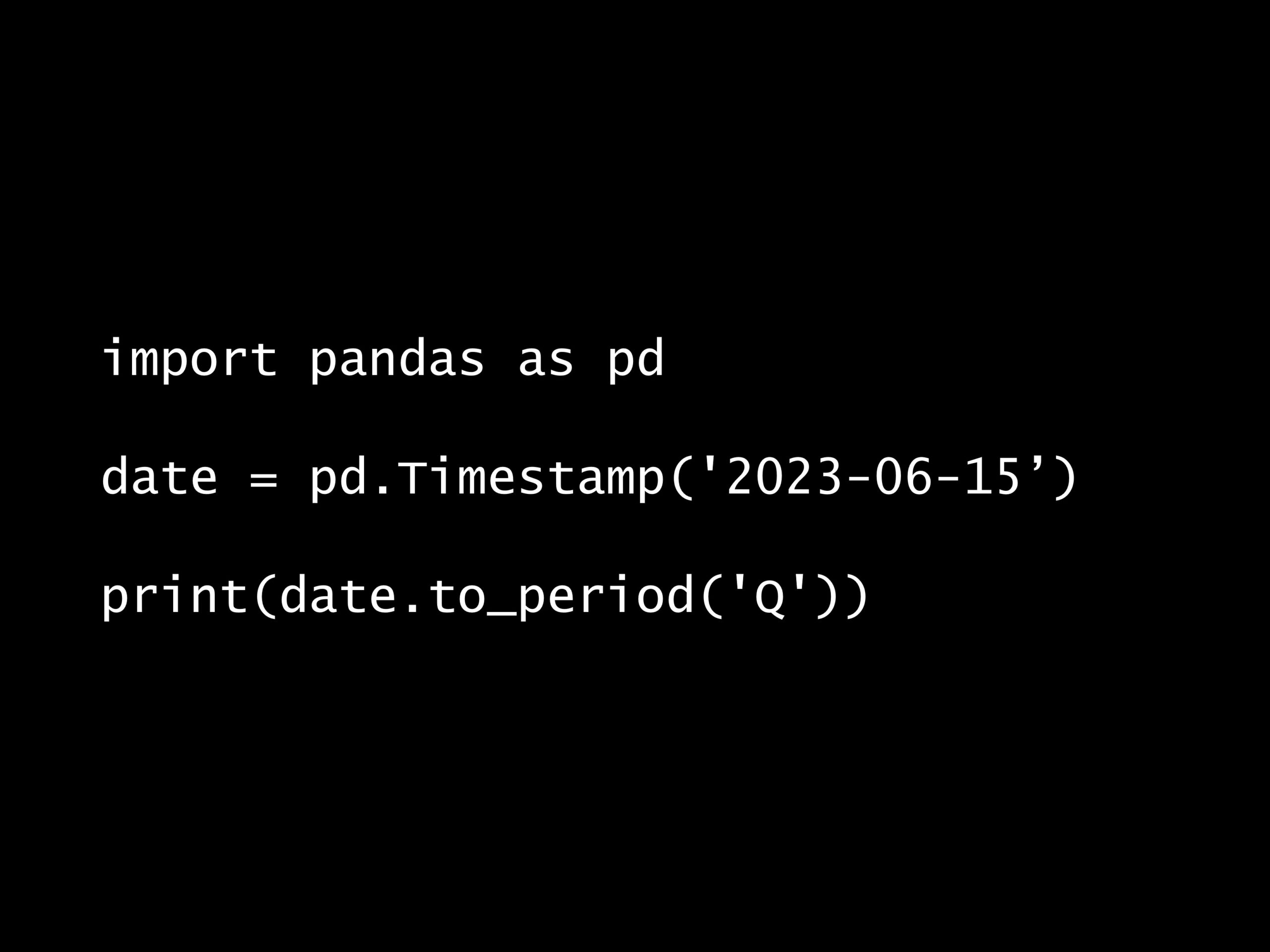
次の Python コードの出力はどれでしょうか? Python コード: import pandas as pd date = pd.Timestamp('2023-06-15') print(date.to_peri...